|
|
结构力学仿真工程师一名,最近在复习刘鸿文的《材料力学》第五版,顺便记一些笔记,每周更新。
第一章 绪论
- 强度要求:构件应该有足够的抵抗破坏的能力,如结构屈服破坏
- 刚度要求:构件应该有足够的抵抗变形的能力,防止结构变形过大,如车门下垂
- 稳定性要求:构件应该有足够的保持原有平衡形态的能力,防止屈曲
2、材料力学基本假设
- 连续性假设:材料连续无空隙
- 均匀性假设:内部晶粒均匀排列
- 各向同性假设:各方向力学性能相同
- 小变形假设:只研究变形远远小于构件的最小尺寸的情况
3、内力和外力:物体因受外力作用而变形,其内部各部分之间因相对位置改变而引起的相互作用就是内力。即使不受外力作用,物体的各质点之间本身也存在作用力,但材料力学研究的是因外力而引起的附加相互作用力,即附加内力
4、材料力学主要研究对象:长度远大于横截面尺寸的杆
5、横截面大小和形状都不变的称等直杆,轴线为直线的称直杆,截面形心的连线称轴线
6、应变:分线应变和切应变
线应变:单位长度的平均伸长或缩短量
切应变:又称角应变,指变形前后角度变化
应力:单位面积受力大小,分正应力和切应力,单位Pa=N/m2
7、基本变形形式:
- 拉伸或压缩:外力作用方向与轴线重合
- 剪切:一对大小相等,方向相反的外力作用于某个截面内
- 扭转:由一对大小相等、转向相反、作用面垂直于杆轴线的力偶引起,表现为杆件的任意两个横截面发生绕轴线的相对转动
- 弯曲:一个或多个力作用于垂直于轴线的平面上,使杆件发生垂直于轴线的变形
第二章 拉伸、压缩与剪切
8、拉应力为正,压应力为负
9、圣维南原理:如用与外力系静力等效的合力来代替原力系,则除在原力系作用区域内 \sigma_{\alpha}=\sigma cos \alpha^{2} 有明显差别外,在离外力作用区域略远处(例如距离约等于横截面尺寸处),上述替代的影响就非常微小,可以不计。
10、等直杆受轴向力拉伸时,横截面上正应力为σ,无剪应力;若取与横截面夹角为α的斜截面,
斜截面上正应力为: \sigma_{\alpha}=\sigma cos^2\alpha
斜截面上剪应力为: \tau_\alpha=\frac{1}{2} \sigma sin2\alpha
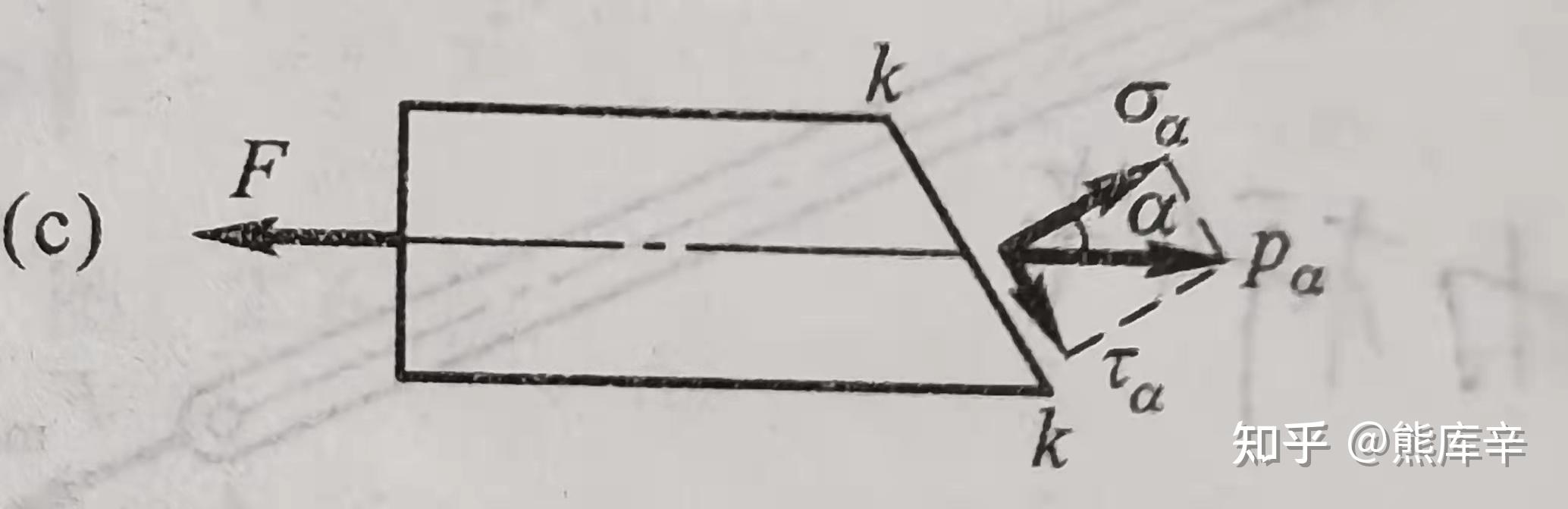
当夹角为45度时,斜截面上剪应力取最大值,为0.5σ,因此拉伸实验时可能会沿着45度斜截面因剪应力过大而发生断裂
11、卸载定律:加载到超过屈服点后,再卸载,卸载过程中,应力-应变按直线规律变化,弹性变形会消失,塑性变形保留,短时间内再次加载,应力应变会沿着卸载曲线上升,但强度极限不变
12、金属热处理工艺
退火:将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却;目的:1)降低硬度,改善切削性能;2)降低残余应力,稳定尺寸,减少变形与裂纹倾向;3)细化晶粒,调整组织,消除组织缺陷;4)均匀组织和成分。
淬火:工件加热奥氏体化后快速冷却获得马氏体或贝氏体组织的热处理工艺。淬火的目的是使过冷奥氏体进行马氏体或贝氏体转变,得到马氏体或贝氏体组织,然后配合以不同温度的回火,以大幅提高钢的刚性、硬度、耐磨性、疲劳强度以及韧性等。
回火:为了降低钢件的脆性,将淬火后的钢件在高于室温而低于710℃的某一适当温度进行长时间的保温,再进行冷却。
正火:将工件加热到适宜的温度后在空气中冷却,正火的效果同退火相似,只是得到的组织更细,常用于改善材料的切削性能。
13、低碳钢:含碳重量占总质量的0.05%-0.3%,强度和硬度较低,塑性和韧性较好,可用卷边、冲压、折弯等工艺进行冷成形;
中碳钢:含碳量为0.3%——0.60%
高碳钢:含碳量0.6%以上,含碳量越高,强度和硬度都相应提升,但伸长率减小,即塑性较差
14、铸铁抗拉强度大约110MPa,抗压强度大约为抗拉强度的4-5倍,为600MPa左右;其他脆性材料,如混凝土、石料与铸铁类似,抗压强度远大于抗拉强度
15、随着测试温度升高,杨氏模量和屈服应力都降低;低温情况下,弹性极限和强度极限都升高,但伸长率减小,碳钢变得更脆。
16、蠕变:高于某一温度(0.3~0.4倍的熔化温度),且应力超过某一限度,则材料在这一固定应力和不变温度下,随着时间的增长,变形将缓慢增大。蠕变是塑性变形,卸载后不再消失。
开始阶段,蠕变速率很高,但速度逐渐降低;然后进入稳定的蠕变阶段;最后蠕变速率急剧增大。
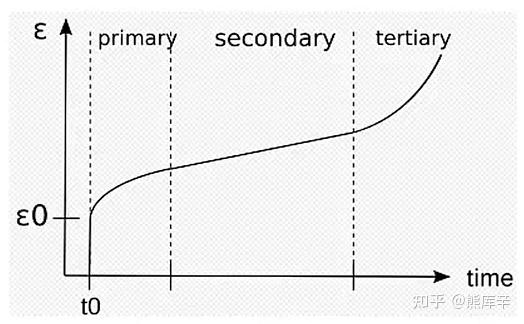
蠕变曲线
应力松弛:是指构件总变形(弹性变形和塑性变形)保持不变,蠕变使塑性变形不断增加,弹性变形相应减少,而应力随时间缓慢降低的现象
17、脆性材料许用应力不超过强度极限,安全因数一般取1.2~2.5;塑性材料强度极限不超过屈服极限,安全因数一般取2~3.5
18、常用材料性能参数
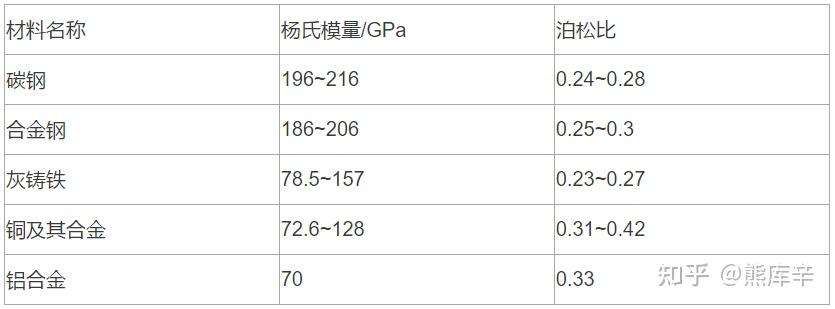
19、泊松比:当应力不超过比例极限时,横向应变和轴向应变之比的绝对值μ=|ϵ'/ϵ|,或者ϵ'=−μϵ
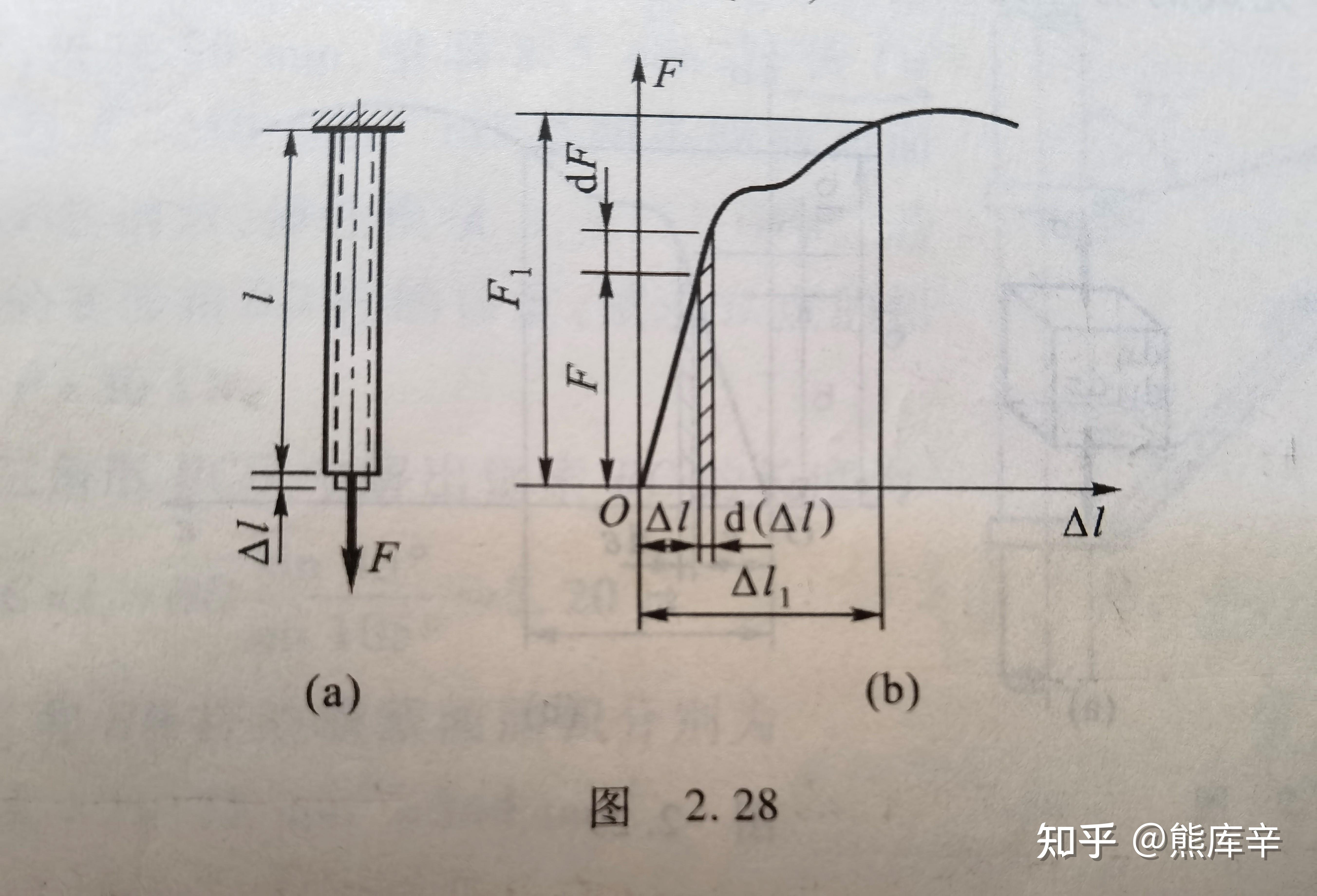
20、应变能:弹性固体在外力任用下,因变形而储存的能量
拉力-变形曲线如下所示,应变能等于拉力做功,弹性范围内拉力做功计算公式如下:
w=0.5FδL
应变能密度(单位体积应变能)计算公式为 v=\frac{1}{2} \frac{F}{A} \frac{\Delta L}{L}=\frac{1}{2}\sigma \epsilon ,其中A*L等于体积
21、静定问题:杆件的轴力可由静力平衡方程求出
超静定问题:对于构件仅用静力平衡方程不能求出全部未知力,通常需要结合静力平衡方程、变形协调方程和物理方程等三方面关系进行求解。核心:静平衡方程(三个方向力平衡+平面转矩平衡)+变形协调方程(拆除造成超静定的约束,用力替换)

22、静定结构温度均匀变化时,可以自由变形,不会引起构件内力;静定结构的构件变形受到部分或全部约束,温度变化往往就会引起内力。
23、应力集中:因外形突然变化而引起的局部应力急剧增大的现象。比如圆孔、轴肩、切口等位置。
设发生应力集中的截面上最大应力为 \sigma_{max} ,同一截面上平均应力为σ,则应力集中度为K=\frac{\sigma_{max}}{\sigma}
脆性材料制成的部件,没有屈服段,可能会直接断裂,因此要尽量避免脆性材料发生应力集中;但灰铸铁因其内部不均匀性和缺陷往往是产生应力集中的主要因素,零件外形改变引起的应力集中只是次要因素。
24、剪切特点:作用于构件某一截面两侧的力,大小相等,方向相反且相互平行,使构件的两部分沿这一截面(剪切面)发生相对错动的变形。工程中的连接件,如受剪的螺栓、螺钉、铆钉、销钉和键等都是主要受剪切的构件。
25、圆柱被挤压时面积计算方法:圆柱直径乘以高度,即圆柱过轴线截面积
第三章 扭转
26、什么是扭转变形?
答:杆件两端各作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动,就是扭转变形。比如与汽车方向盘相连的转向轴、拧紧过程中的螺栓、汽车传动轴等部件都承受扭矩。材料力学只研究圆截面等直杆的扭转变形,以扭转变形为主的杆件常称为轴。
27、电机扭矩计算公式
设电机输出功率为P(kW),转速为n(r/min),输出扭矩为Me(N.m),则 2\pi*\frac{n}{60}*M_e=2\pi*\frac{n}{60}*R*F=P*1000 ,则扭矩计算公式 M_e=9549*\frac{P}{n}
其中 2\pi*\frac{n}{60}*R 等于轴表面一点转动的距离
28、扭矩正负号规定:按右手螺旋法则把T表示为矢量,当矢量方向与所研究部分中截面的外法线的方向一致时,T为正,反之为负。
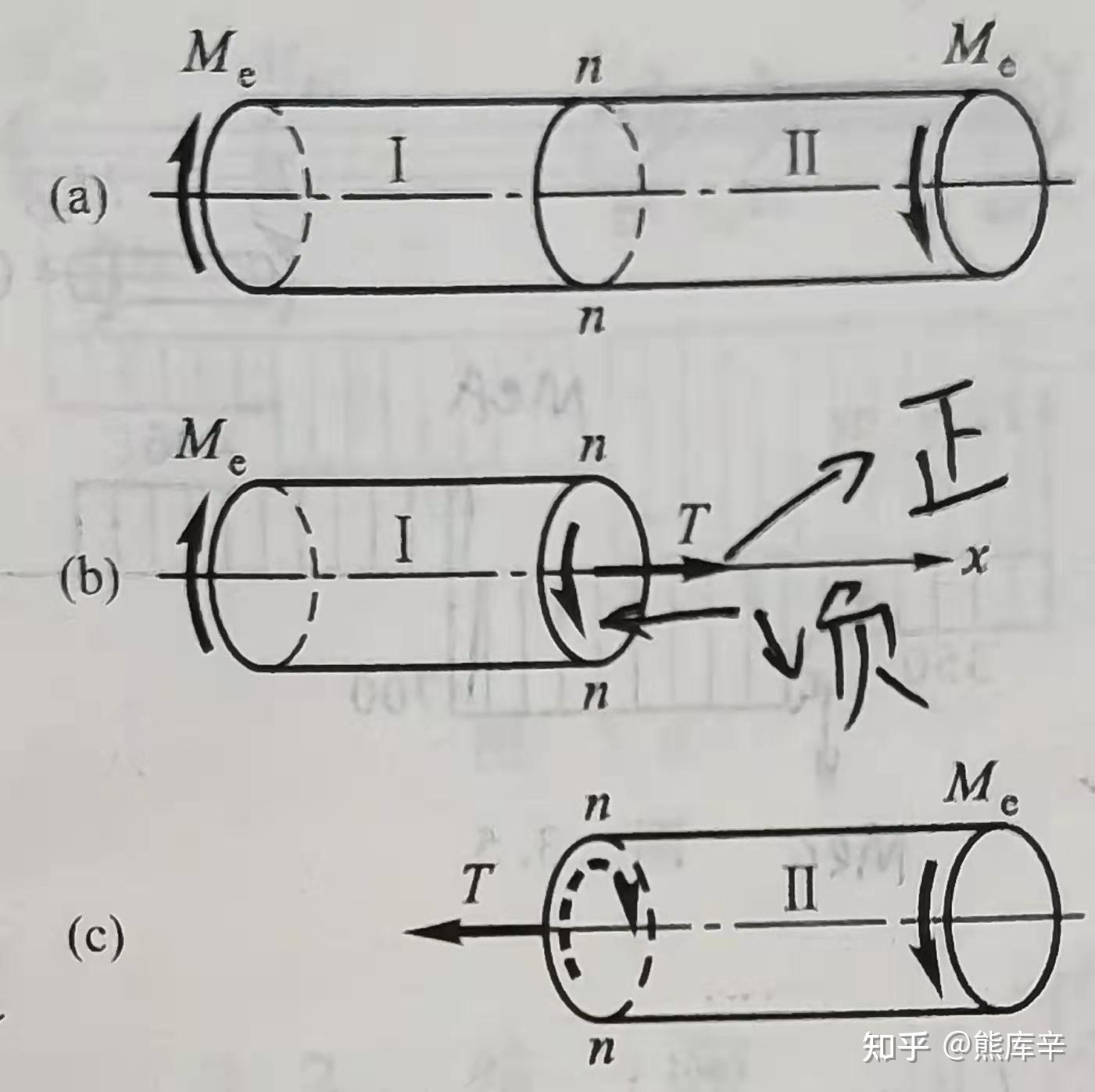
29、薄壁圆筒:内径除以壁厚大于10。
很薄,厚度方向应力变化可以忽略,
30、薄壁圆筒扭转时切应力计算公式
M_e=2\pi r\delta*\tau*r =截面积*切应力*半径
切应力\tau=\frac{M_e}{2\pi r^2\delta}
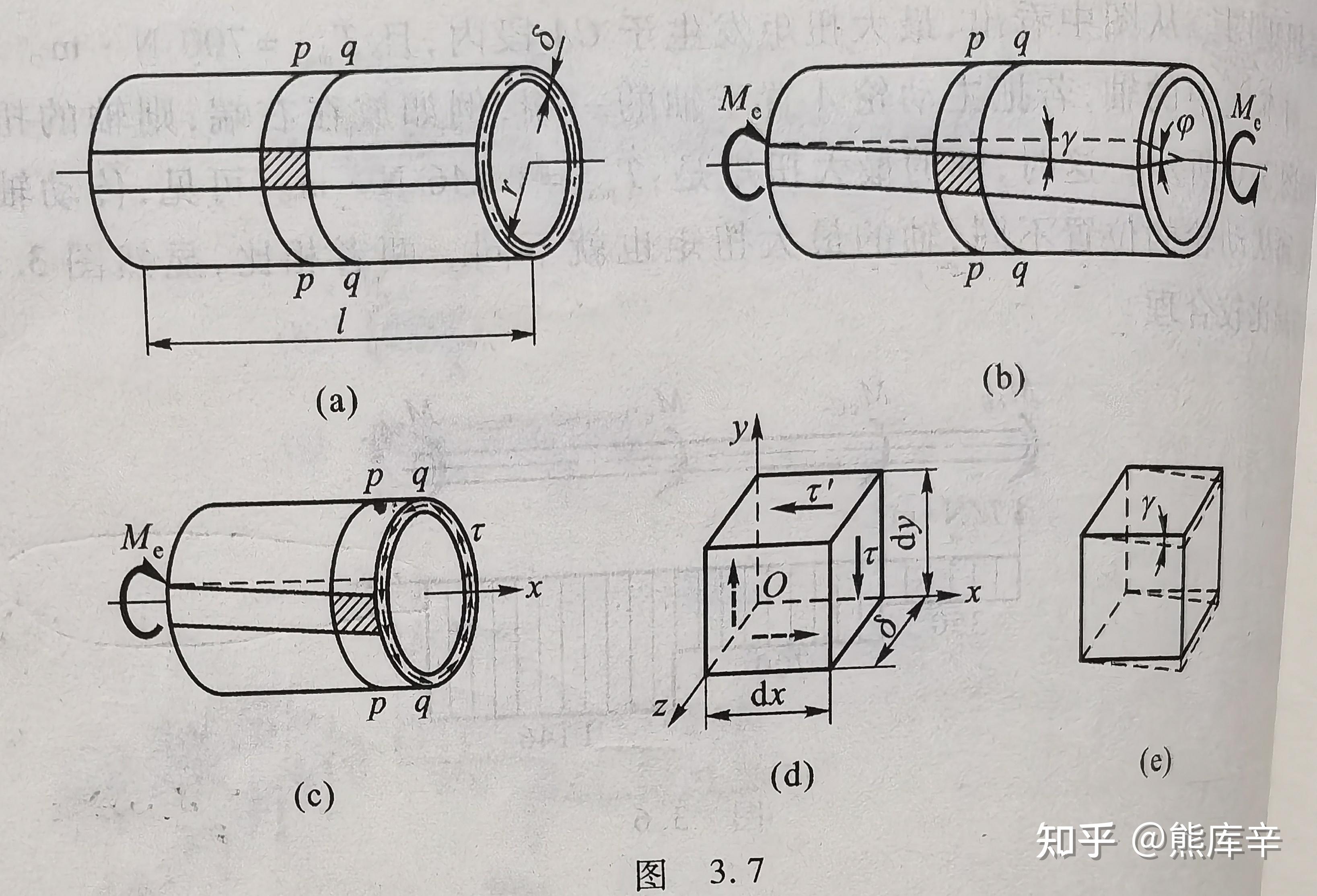
切应力互等定理:在单元体相互垂直的两个平面上,切应力必然成对存在,且数值相等;两者都垂直于两个平面的交线,方向则共同指向或共同背离这一交线。
由力偶平衡方程有:
(\tau \delta dy)dx=(\tau'\delta dx)dy
可以推出切应力互等定理
τ=τ′
31、纯剪切:只有切应力,没有正应力;
主应力:微元体六个面上只有正应力,没有剪应力,三个正应力考虑正负情况下,数值最大的为第一主应力,数值最小的为第三主应力,另一个为第二主应力
切应变定义:纯剪切单元体的相对两侧面发生微小的相对错动(参考下图),使原来互相垂直的两个棱边的夹角改变了一个微量γ,即切应力
切应变计算公式(参考下图)
\gamma = \frac{r\varphi}{l}
rφ为弧长,l为半径,弧长除以半径等于夹角
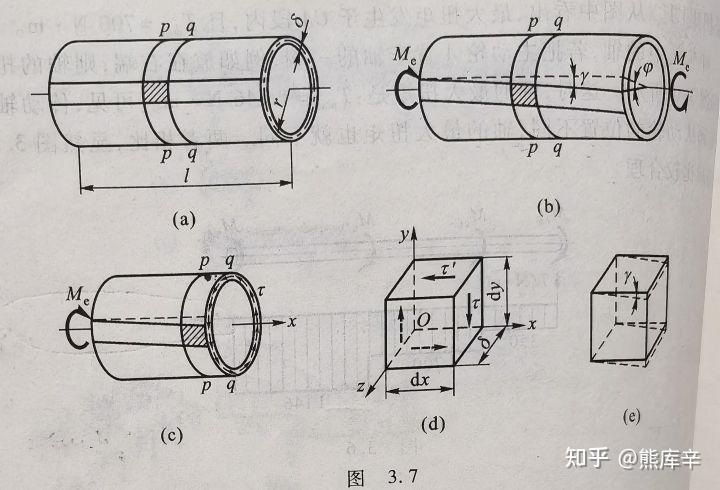
切应变示意图
32、剪切胡克定律:当切应力不超过材料的剪切比例极限时,切应变与切应力成正比,有τ=Gγ,切应变γ没有量纲,因此剪切模量G单位与切应力相同,为MPa。弹性模量,泊松比和剪切模量三者间关系: G=\frac{E}{2(1+\mu)}
33、拉伸工况下,应变能密度为 v=\frac{1}{2}\sigma\epsilon ,可推出,纯剪切情况下,应变能密度 v=\frac{1}{2}\tau\gamma ,由剪切胡克定律有v=\frac{1}{2}\tau\gamma=\tau^2/2G
34、圆轴扭转平面假设:等直圆轴扭转变形前原为平面的横截面,变形后仍保持为平面,形状和大小不变,半径仍保持为直线;且相邻两横截面间的距离不变
35、圆轴扭转时的应变,此时圆轴处于纯剪切状态,只有下图b中的切应变γ,没有正应变;切应变计算公式如下: \gamma_\rho=\rho\frac{d\phi}{dx}
\rho d_\phi 表示矩形ab边的扭转弧长aa'=圆轴半径乘以扭转角幅度;dx表示矩形abcd的长度,相当于矩形扭转时的半径,幅长除以半径即可得到扭转角(单位为幅度);当ρ=R时,表示圆轴表面的切应变;
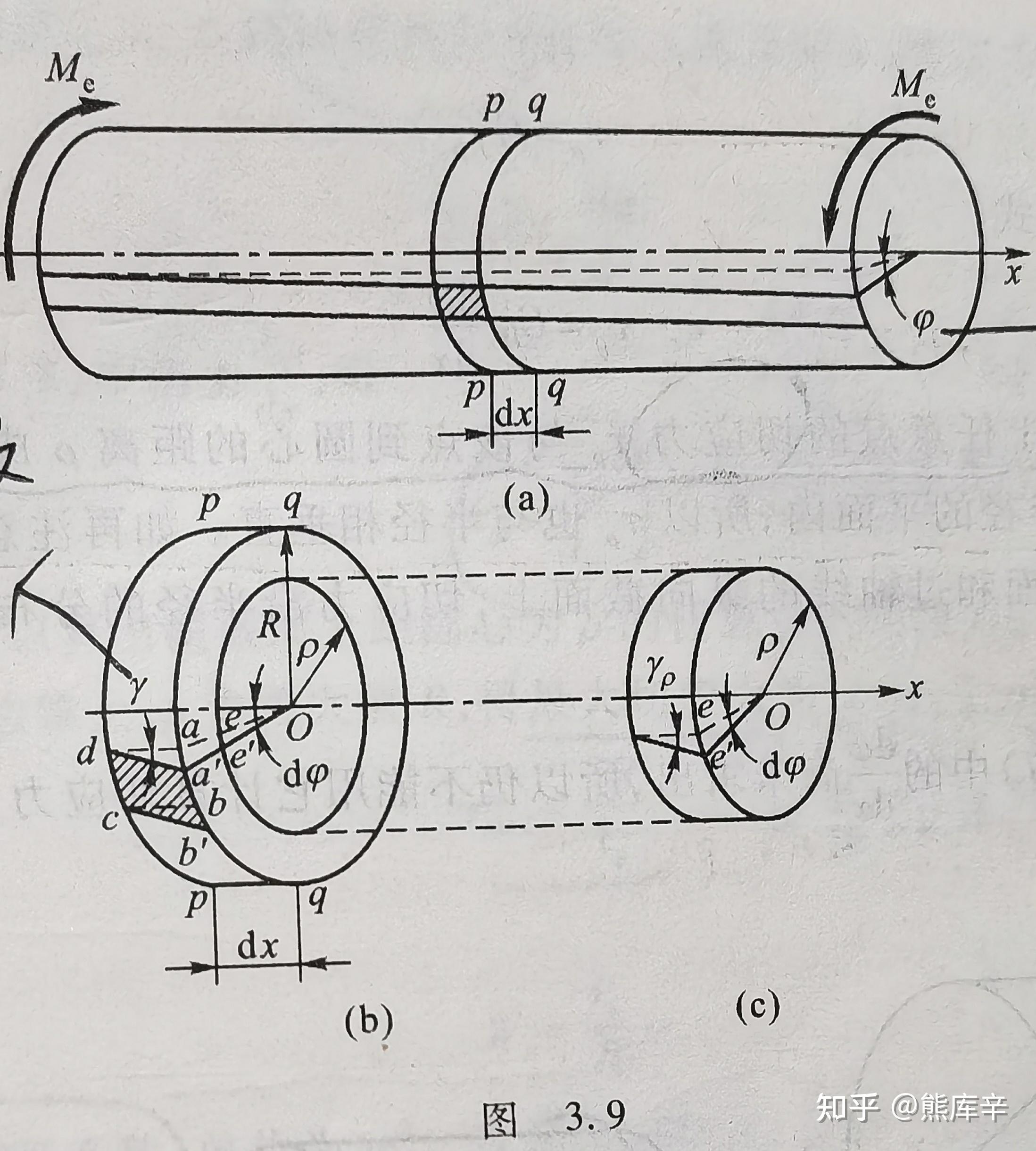
35、实心圆轴扭转时切应力计算公式如下,切应力随着ρ增大而增;最大切应力在圆轴表面,轴心位置切应力为零,实心圆轴材料利用率低;因此一般做成圆管或方管,不做实心结构。
\tau_\rho=G\gamma_\rho=G\rho\frac{d\phi}{dx}
上述切应力计算公式中含有求微分项,无法直接得知切应力,需要借助静力平衡关系进行求解;
通过电机功率和转速可计算出圆轴扭矩,若用应力乘以面积对圆心求矩,然后积分同样可得圆轴任意截面上的扭矩,两式相等即可得到切应力的具体计算公式,切应力推导公式如下:
T=\int_{A}\rho\tau_\rho dA=G\frac{d\phi}{dx}\int_{A}\rho^2 dA=GI_p\frac{d\phi}{dx}
联立切应力公式,得切应力求解公式,当ρ取最大值R时,可得表面最大切应力求解公式,
\tau_{\rho}=\frac{T\rho}{I_p}=\frac{TR}{I_p}=\frac{T}{W_t} , W_t=\frac{I_p}{R} 为圆轴抗扭截面系数
I_p 称为横截面对圆心的极惯性矩(截面二次矩),单位为米的四次方;
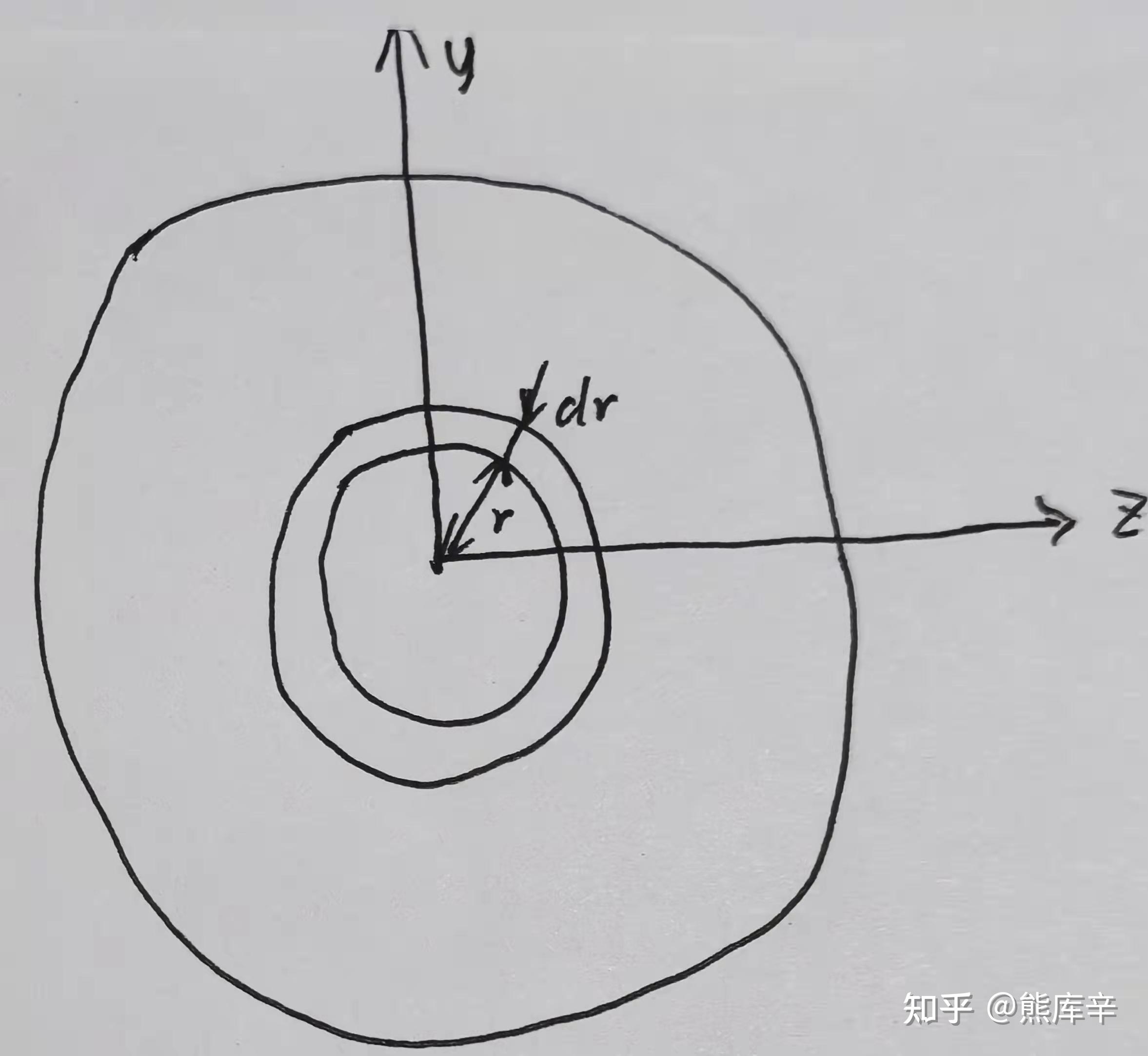
实心圆轴横截面对圆心极惯性矩为:I_p=\int_{A}\rho^2dA=\int_{0}^{2\pi}\int_{0}^{R}\rho^3d\rho d\theta=\frac{\pi R^4}{2}=\frac{\pi D^4}{32}
另一种方法求圆轴横截面对圆心的极惯性矩:dA取下图所示的圆环,则微元面积 dA=2\pi \rho *d\rho ,即内径乘以宽度;因此 I_p=\int_{A}\rho^2dA=\int_{0}^{R} 2\pi\rho^3d\rho=\frac{\pi R^4}{2}
同理,空心圆轴截面对圆心的极惯性矩为 I_p=\int_{A}\rho^2dA=\int_{d/2}^{D/2} 2\pi\rho^3d\rho=\frac{\pi(D^4-d^4)}{32}
实心圆轴抗扭截面系数: W_t=\frac{I_p}{R}=\frac{\pi D^3}{16}
空心圆轴抗扭截面系数: W_t=\frac{I_p}{R}=\frac{\pi(D^4-d^4)}{32}=\frac{\pi D^3(1-\alpha^4)}{16} ,其中 \alpha=\frac{d}{D}
若希望实心圆轴和空心圆轴有相同的抗扭强度,令两轴的抗扭截面系数相等即可;对比可发现,相同抗扭截面系数时,空心圆轴外径更大,但空心圆轴截面积明显小于实心圆轴
36、扭转角计算公式, GI_p 又称为抗扭刚度;扭转角度和扭矩成正比,与轴长度成正比。
\phi=\frac{Tl}{GI_p}
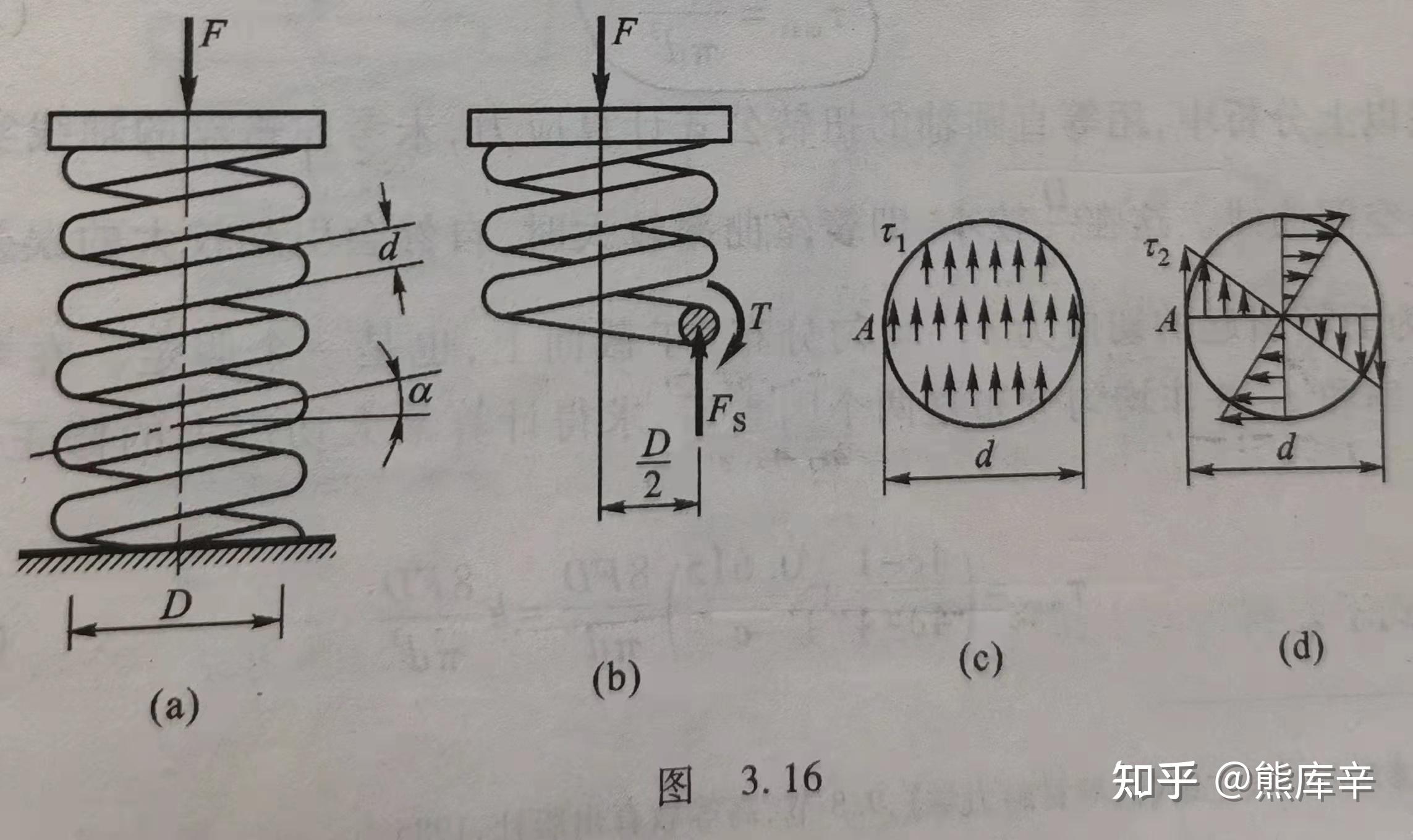
37、螺旋弹簧应力计算——简直牛逼
弹簧截面上应力由两部分构成, F_s 造成的切应力 \tau_1 ,扭矩 T 造成的扭转切应力 \tau_2 ,下图(c)中的A点达到最大值 \tau_1+\tau_2 ,粗略估计的切应力计算公式为
\tau=\tau_1+\tau_2=\frac{F_s}{A}+\frac{T}{W_t}=\frac{4F}{\pi d^2}+\frac{8FD}{\pi d^3}=\frac{8FD}{\pi d^3}(\frac{d}{2D}+1) ,当 \frac{D}{d} 大于等于10时,上式中的 \frac{d}{2D} 可以忽略。
螺旋弹簧精确计算公式为 \tau_{max}=(\frac{4c-1}{4c-4}+\frac{0.615}{c})\frac{8FD}{\pi d^3}=k\frac{8FD}{\pi d^3} ,其中 c=\frac{D}{d}, k=\frac{4c-1}{4c-4}+\frac{0.615}{c} ,c越小,k越大,粗略计算公式误差越大
38、通过能量法,外力功=弹簧本身存储的应变能,可以求解弹簧刚度 K=\frac{Gd^4}{8D^3n} ,其中G表示剪切模量,d表示簧丝直径,D表示弹簧圈直径,n表示扣除两端与簧座接触部分后的有效圈数
39、非圆截面扭转:
- 自由扭转:等直杆两端受扭转力偶作用且翘曲不受任何限制
- 约束扭转:由于约束条件或受力条件的限制,杆件各横截面的翘曲程度不同,势必引起相邻横截面间纵向线段的长度改变,从而导致横截面上除了切应力外还有正应力;工字梁和槽钢等薄壁件,约束扭转时横截面上正应力相当大,但矩形或椭圆截面杆件,约束扭转正应力很小,与自由扭转没有明显区别。
第四章 弯曲内力
40、以弯曲变形为主的杆件,习惯上称为梁;以扭转变形为主的杆件,习惯上称为轴;
41、对称弯曲:当作用于杆件上的所有外力都在纵向对称面内时,弯曲变形后的轴线也将是位于这个对称面内的一条曲线
42、什么情况下可以将载荷简化为集中力?
答:实际零件大多受分布载荷,非集中力,当分布载荷分布的范围远小于零件本身总体尺寸时,可以将分布力简化为集中力,根据圣维南原理,将分布载荷简化为集中力只会影响局部受力情况,并不会影响全局受力。
43、梁形式分类
悬臂梁:一端固定, 一端自由

简支梁:一端固定铰支座(水平和竖直方向不能移动,可转动),一端为滑动铰支座(竖直方向不能动,水平方向可移动)

外伸梁:一个固定铰支座约束(水平和竖直方向不能移动,可转动),一端滑动铰支座(竖直方向不能动,水平方向可移动),一侧或者两侧可以外伸

静定梁:支座约束力均可由静力平衡方程完全确定,统称为静定梁;支座约束力不能完全由静力平衡方程确定的梁,称为超静定梁
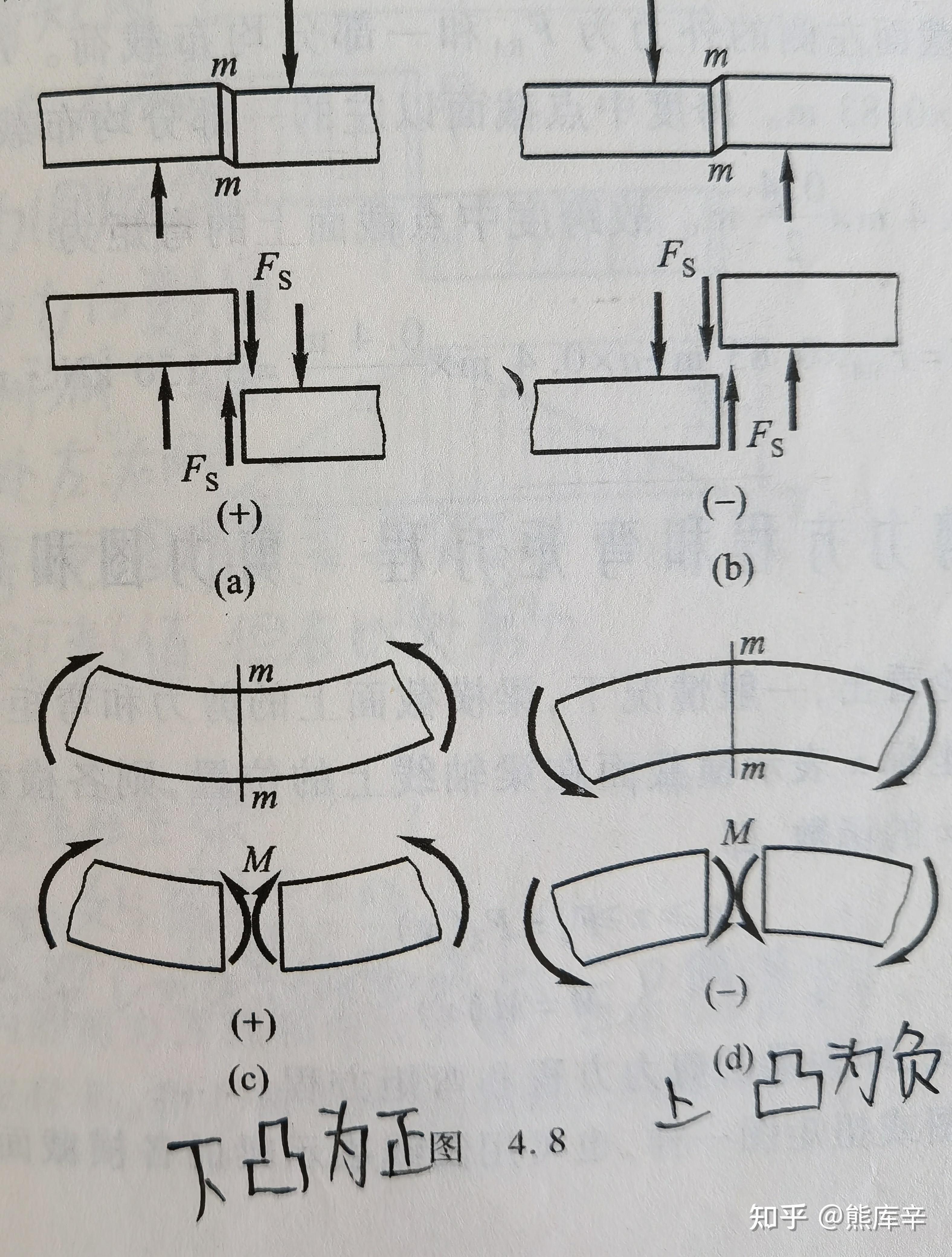
44、绘图时以平行于梁轴的横坐标x表示横截面的位置,以纵坐标表示相应截面上的剪力或弯矩,这种图线分别称为剪力图和弯矩图;
集中力作用截面的两侧,剪力有一突然变化,变化的数值等于集中力;
集中力作用截面的两侧,弯矩有一突然变化,变化的数值等于集中力偶之矩;
现实世界中,不存在集中力/集中力偶,力和力矩都有一定的作用面积或作用线,因此不存在剪力突然的情况;材料力学中将分布载荷简化为集中力只为简化过程;
仿真分析中,若将分布载荷简化为集中力/集中力矩,也会存在剪力/力矩突变的情况,因此集中力附近截面上的剪力和力矩都是不准确的。
45、剪力正负号规定:左段相对右段向上错动时,截面m-m上的剪力为正,反之为负;即左上右下为正,左下右上为负;
弯矩正负号规定:截面m-m处弯曲变形凸向下时,截面m-m上的弯矩规定为正,反之为负;即下凸为正,上凸为负;
此规定只为计算过程方便,以及做剪力图时有统一规则,实际做仿真时没有意义。
第五章 弯曲应力
46、梁发生弯曲时,截面上一般存在弯矩和剪力
弯矩:垂直于横截面的内力系的合力偶之矩,弯矩只与横截面上的正应力相关
剪力:切于横截面的内力系的合力,剪力只与横截面内的切应力相关
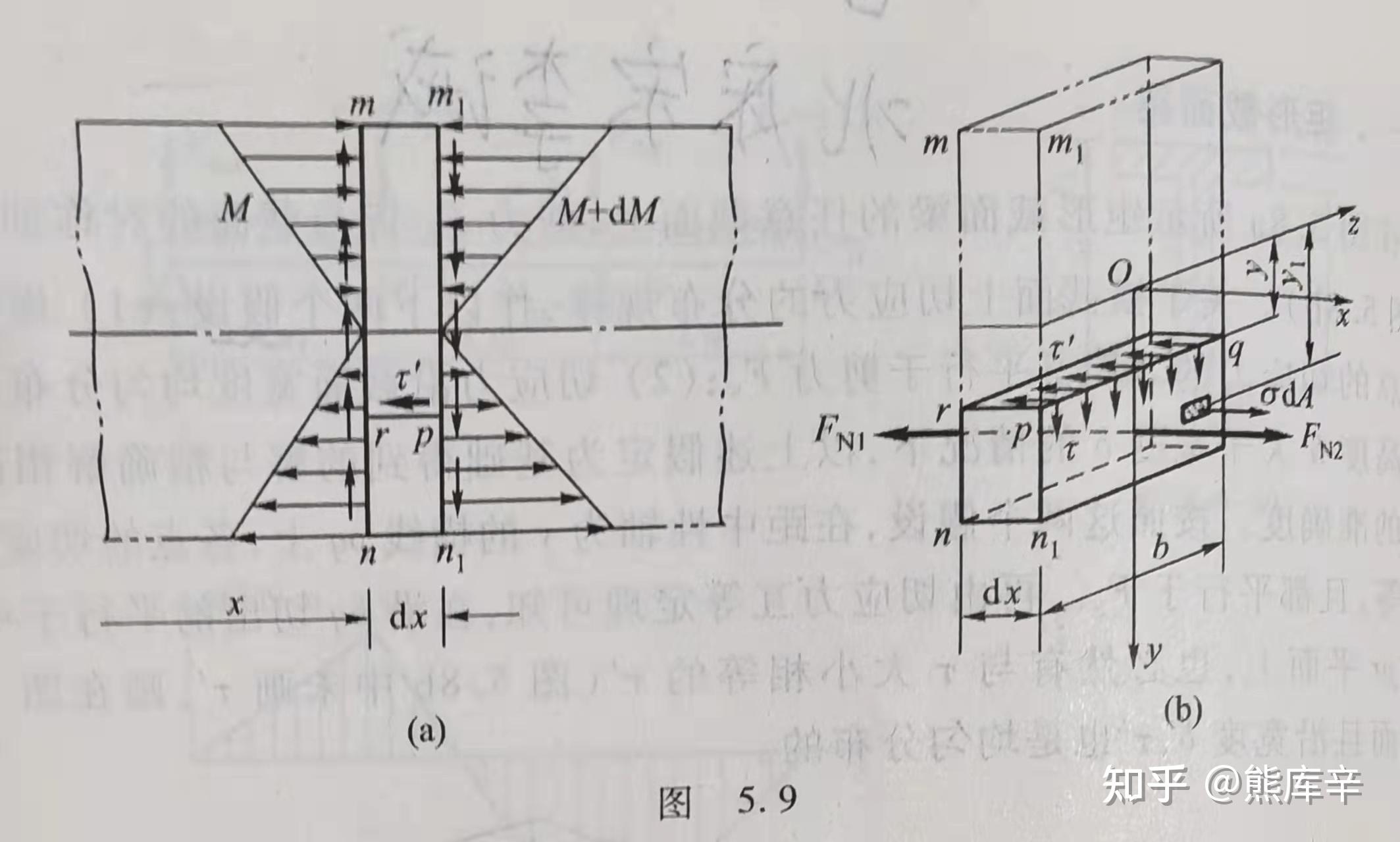
47、纯弯曲:横截面上只有弯矩,没有剪力,即横截面上只有正应力,没有切应力,下图中CD段即为纯弯曲;
横力弯曲/剪力弯曲:横截面上既有弯矩,又有剪力,横截面上既有正应力,又有切应力,下图中AC和DB段即为横力弯曲;
问:还有哪些情况会出现纯弯曲?
答:在梁的纵向对称面内,只作用大小相等、转向相反的一对力偶,梁会发生纯弯曲。
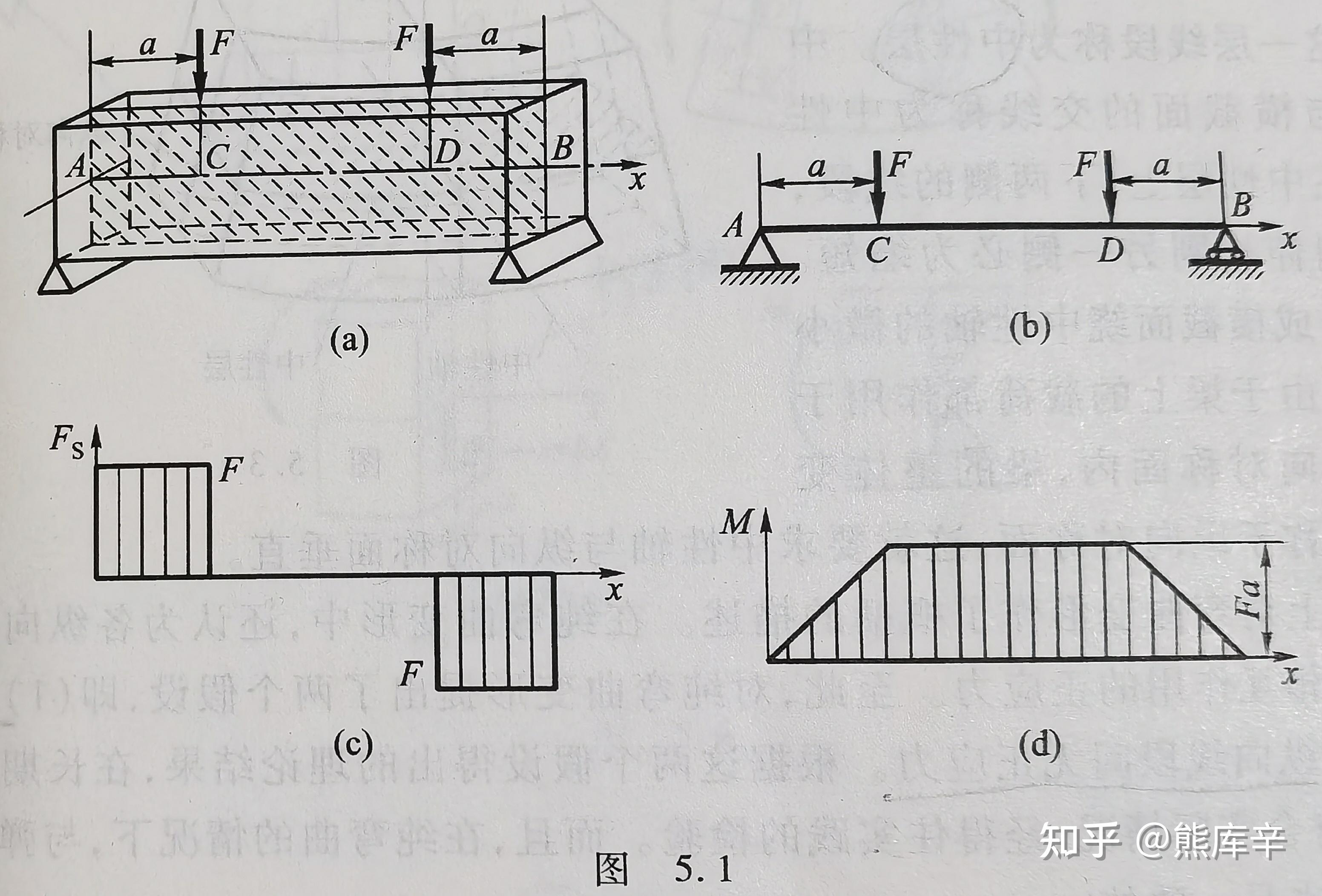
纯弯曲梁
48、弯曲变形的平面假设:变形前原为平面的梁的横截面变形后仍保持为平面,且仍然垂直于变形后的梁轴线
49、纯弯曲变形时的变形几何关系:图(a)中的线段bb变形后为b'b',变长了;
线段bb位置应变为: \epsilon=\frac{b'b'-bb}{bb}=\frac{(\rho+y)d\theta-\rho d\theta}{\rho d\theta}=\frac{y}{\rho}
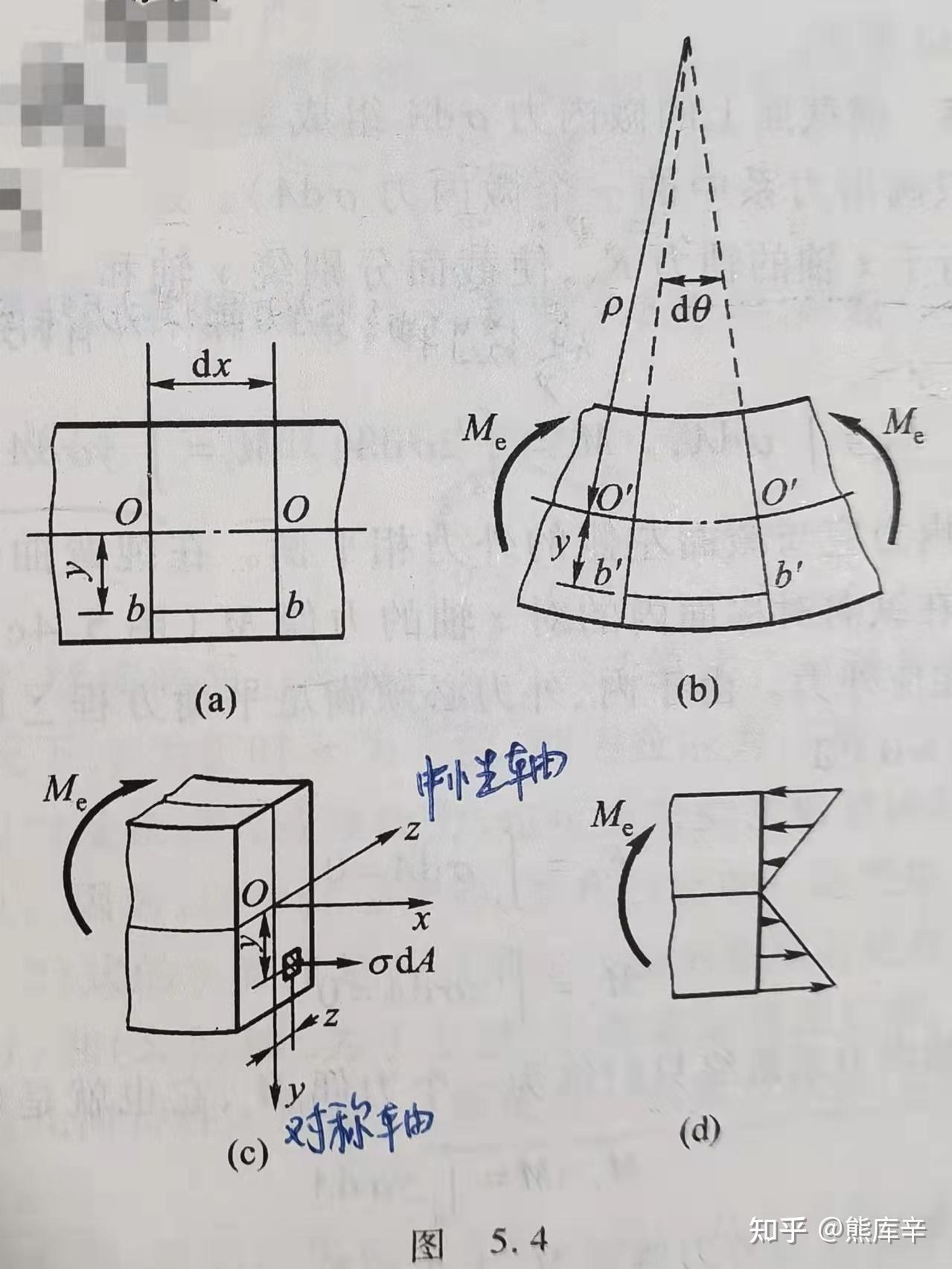
纯弯曲截面受力示意图
物理关系:小变形情况下,应力应变满足胡克定律, \sigma=E\epsilon=E\frac{y}{\rho} ,纯弯曲梁截面上下表面应力最大;扭转变形时,扭转截面上靠近表面位置切应力最大;拉压变形时整个截面上应力相同;事实上绝大多数零件最大应力都出现在表面,因此计算应力时应重点关注表面应力,若模型采用四面体网格建模,表面网格可划分更小尺寸,内部网格可以适当加粗,在保证精度的情况下减小计算量。
静力平衡关系:图5.4(c)中的截面内只有正应力,没有切应力,由静力平衡方程可得,外力偶Me与正应力对Z轴取矩相等 M_e=\int_{A}y\sigma dA=\frac{E}{\rho}\int_{A}y^2dA ,I_z=\int_{A}y^2dA 为横截面对Z轴的惯性矩
结构物理关系可求得纯弯曲变形时,截面正应力为 \sigma=\frac{M_ey}{I_z}=\frac{M_e}{W} ,W为抗弯截面系数,与横截面形状有关;
矩形截面轴惯性矩计算方法:取微元面积 dA 取下图所示长条,则 dA=bdy ,因此 I_z=\int_{A}y^2dA =\int_{-h/2}^{h/2}by^2dy=\frac{bh^3}{12}
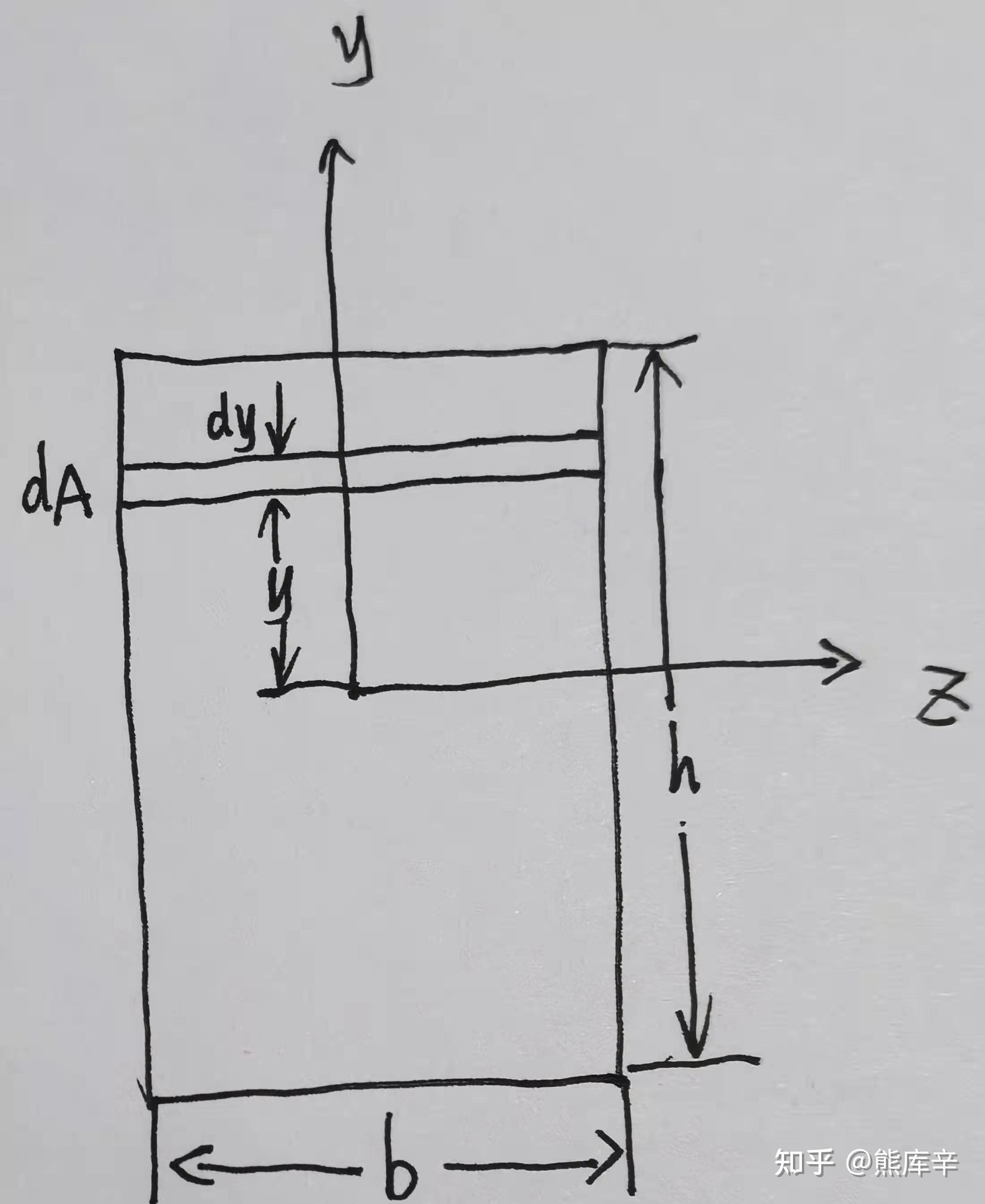
由上式可知,横截面接近上下表面位置y绝对值最大,因此正应力最大。
若横截面是高为h,宽为b的矩形,则横截面对Z轴的抗弯截面系数为,高h对应图5.4中的y轴,宽b对应图5.4中的z轴,由抗弯截面系数计算公式 W=\frac{I_z}{h/2}=\frac{bh^3/12}{h/2}=\frac{bh^2}{6} 可知,抗弯截面系数与受高度影响更大,受宽度影响较小;
若横截面是直径为d的圆形,则抗弯截面系数为 W=\frac{I_z}{d/2}=\frac{\pi d^4/64}{d/2}=\frac{\pi d^3}{32}
50、横力弯曲时,梁横截面上既有弯矩又有剪力,即横截面上既有正应力又有切应力;
对于矩形梁截面,最大正应力在梁的上下表面位置,最大切应力在高度一半的水平截面内,即下式中y=0时,切应力取最大值;Fs为根据力平衡方程计算出的截面上总的剪力;
剪力计算公式 \tau=\frac{F_s}{2I_z}(\frac{h^2}{4}-y^2)=\frac{6F_s}{bh^3}(\frac{h^2}{4}-y^2),y=0时,\tau_{max}=\frac{3}{2}\frac{F_s}{bh}
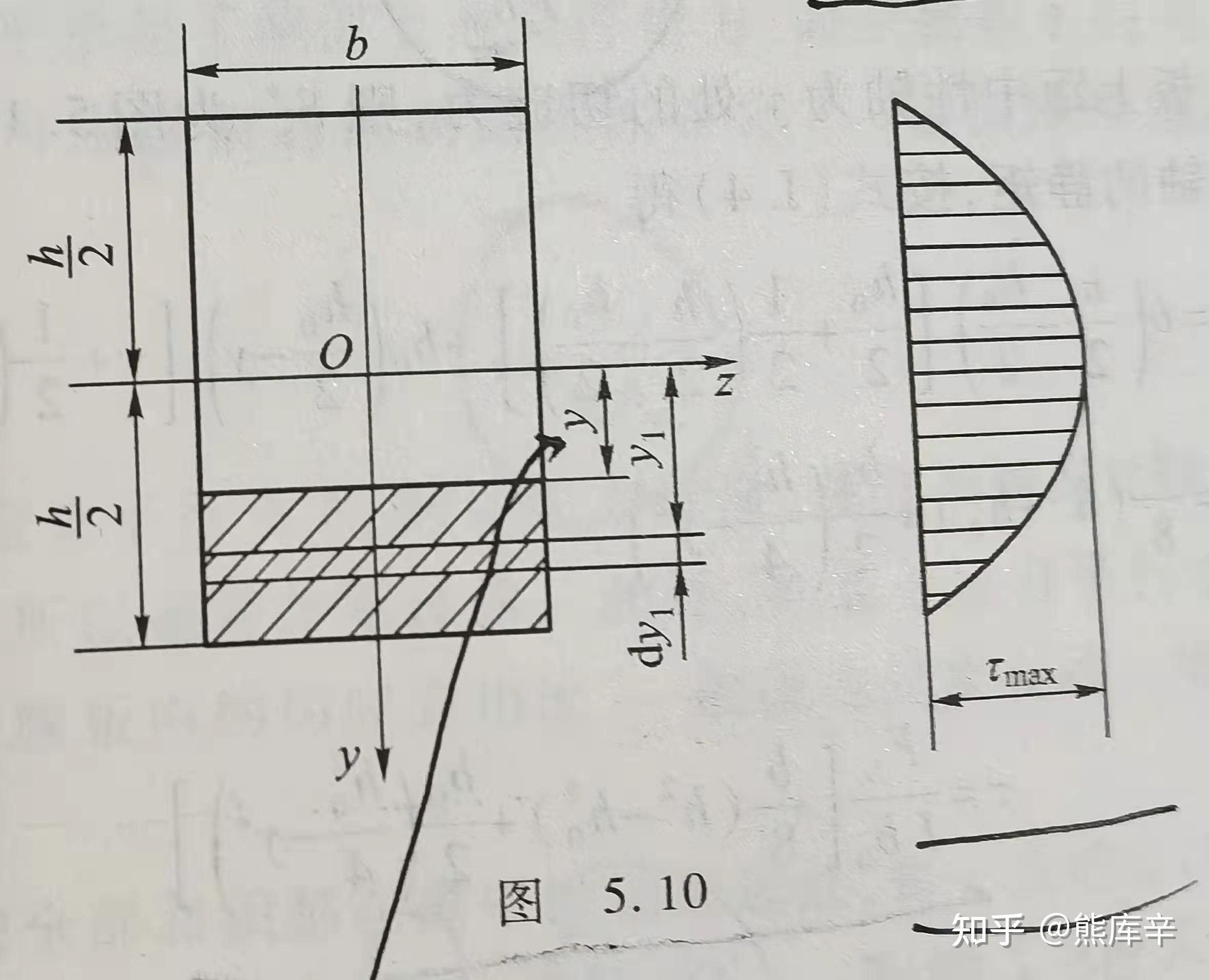
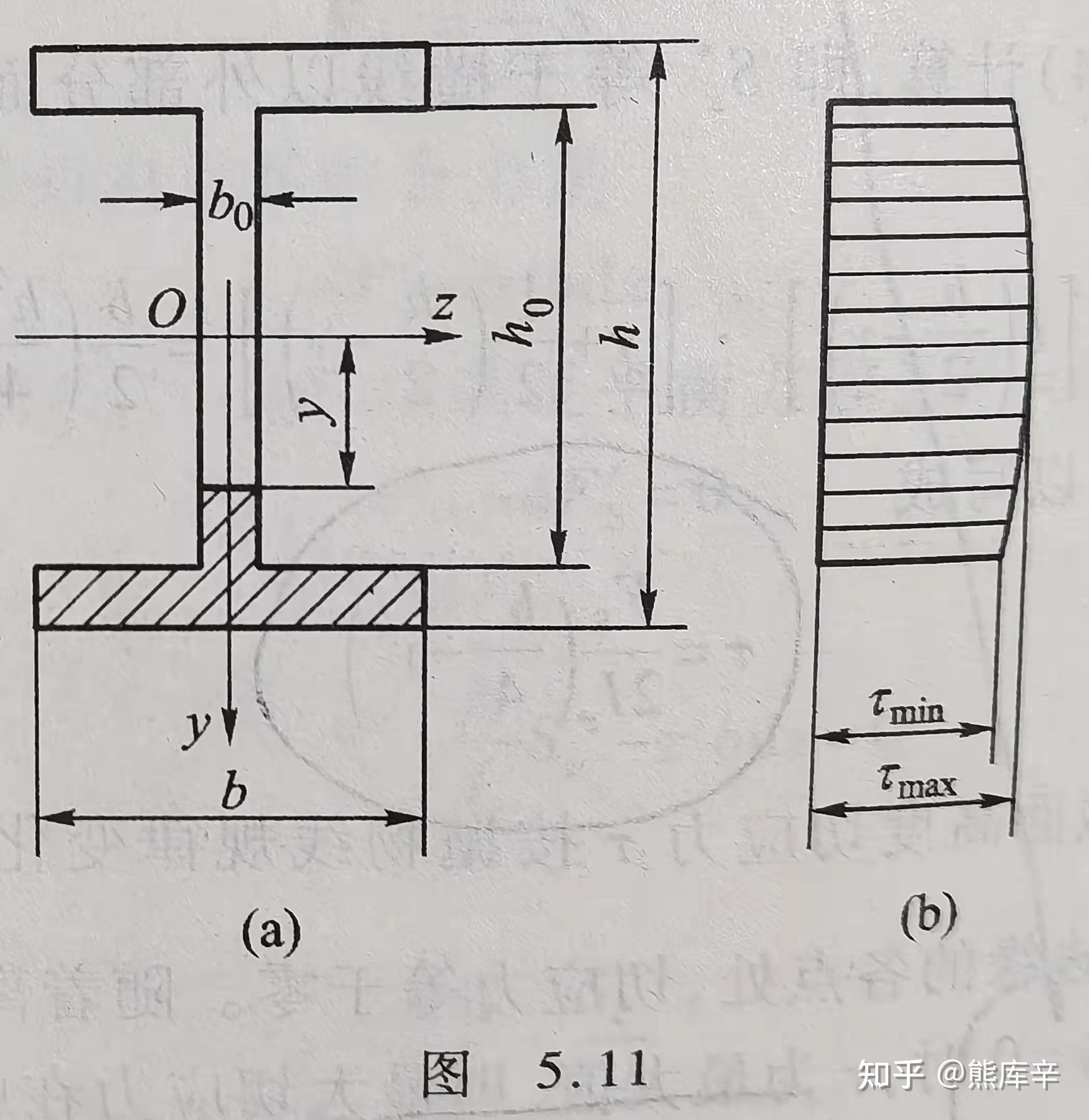
工字梁上腹板承受了绝大部分剪力,腹板上切应力较大,且剪力在腹板上几乎均匀分布,相当于截取图5.10剪应力分布图的中间部分;翼缘承受了截面上绝大部分弯矩,翼缘上正应力很大;根据弯矩和剪力分布图可知,工字梁上每个位置都承载了很大的力,材料使用效率较矩形梁截面高很多,因此工程上得到了大量的应用
腹板上剪力简化计算公式为 \tau=\frac{F_s}{b_0h_0}
51、细长梁一般切应力较小,而正应力较大,强度校核时应重点关注正应力。
在下面三种情况下,应关注梁的切应力:
- 梁的跨度较短(短梁:跨度L和高度H比值在2~5之间),或在支座附近作用较大的载荷,以致梁的弯矩较小,而剪力颇大;
- 铆接或焊接的工字梁,如腹板较薄而截面高度H颇大,因腹板上切应力较大,导致H/2位置切应力很大;
- 经焊接、铆接或胶合而成的梁,对焊缝、铆钉或胶合面,一般要校核剪切强度
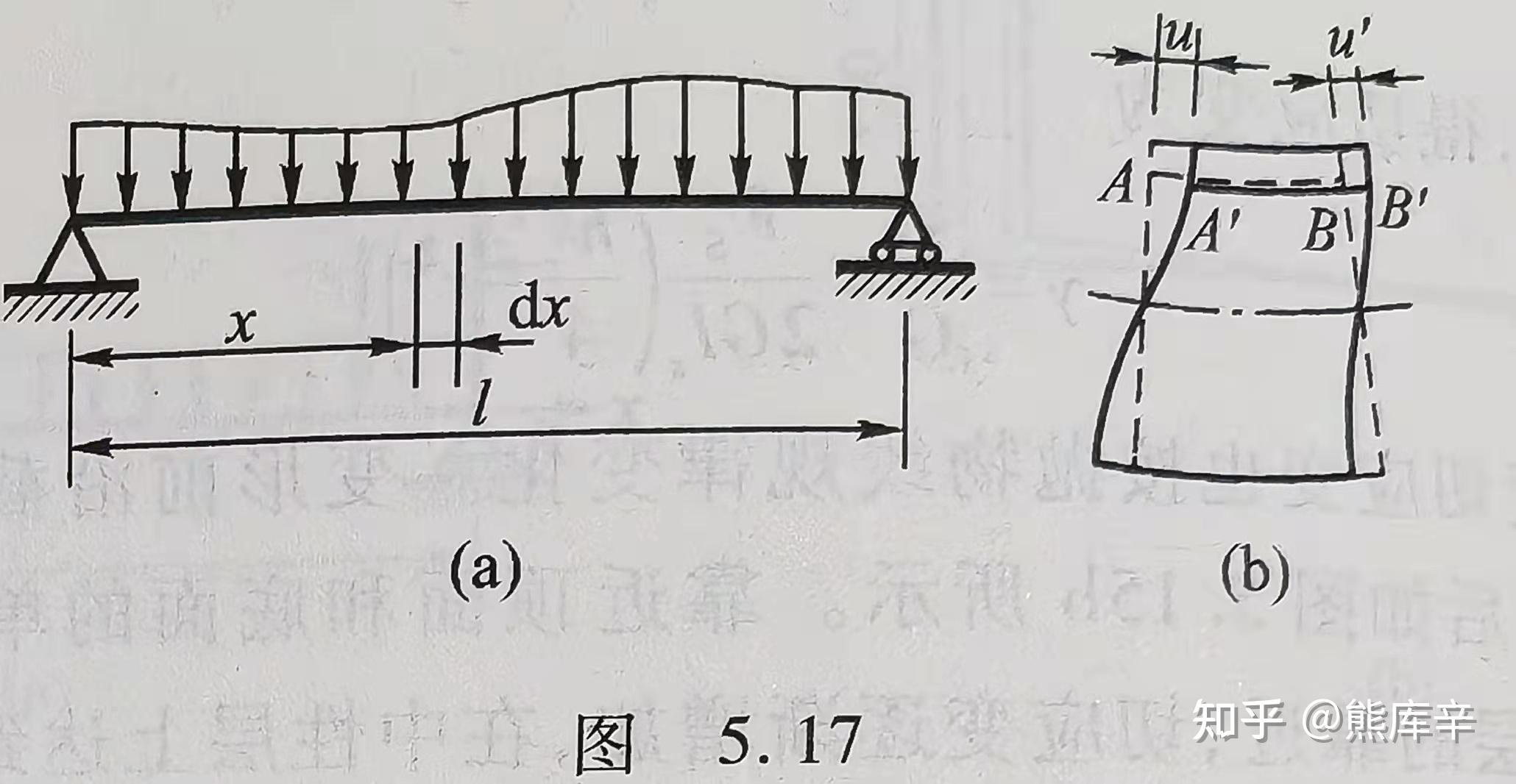
52、横力弯曲时,若剪力随截面位置而变化,相邻两截面上的切应力不同,于是翘曲的程度也不一样;纵向线段AB两端的位移u和u'不相等,线段长度将发生变化,从而引起附加的正应力,导致平面假设不成立,但对于长度远大于截面高度的细长梁而言,附加的正应力非常小,可直接忽略
53、如何提高梁的承载能力?
根据弯曲变形时截面上正应力计算公式 \sigma=\frac{M_ey}{I_z}=\frac{M_e}{W} 可知,截面应力与弯矩和抗弯截面系数有关;若要提高梁的承载能力,应从两方面考虑:一是降低梁上最大弯矩;二是优化截面形状,提高W数值
降低梁上最大弯矩:
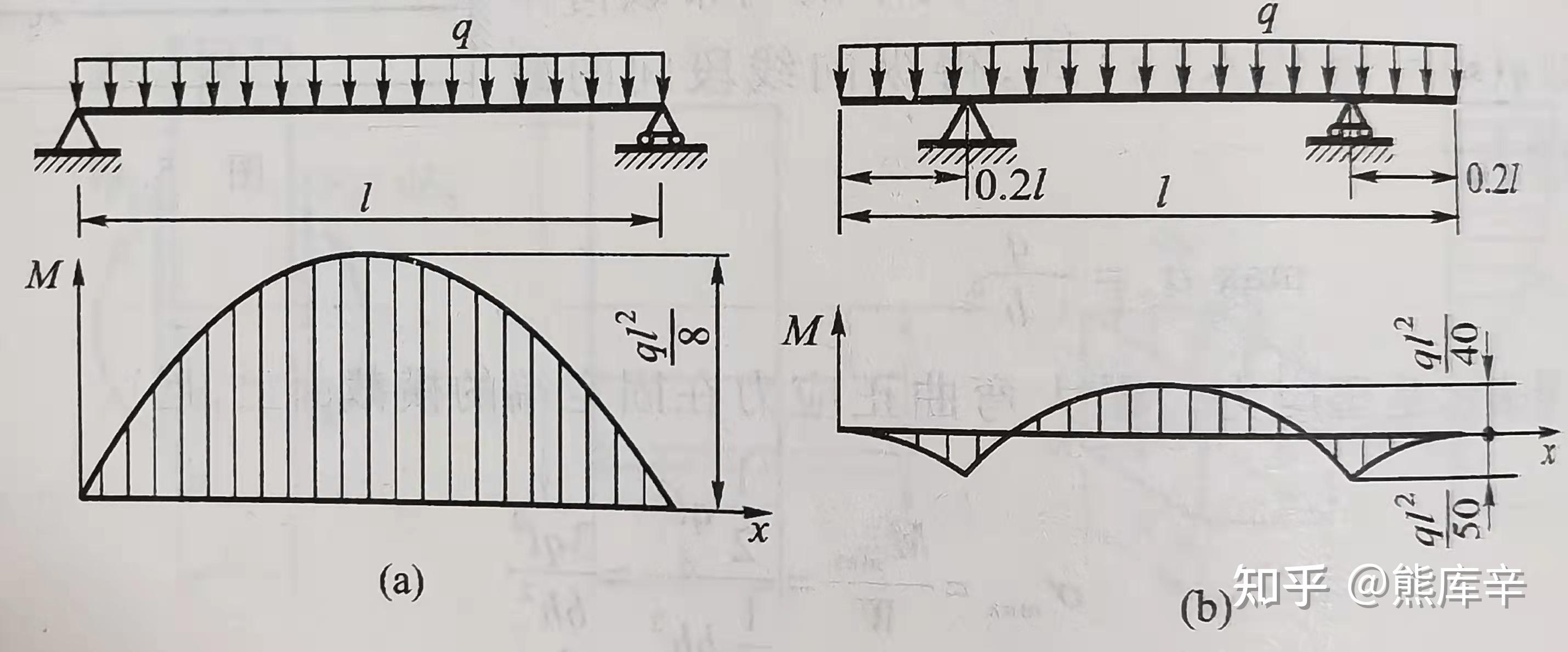
下图(a)中最大弯矩为 M_{max}=\frac{1}{8}ql^2
将两端支座各向里移动0.2L,得到下图(b),下图(b)中最大弯矩减小为 M_{max}=\frac{1}{40}ql^2
由此可知,只是移动了支承位置,承载能力提高4倍
选择合适的梁截面形状,提高抗弯截面系数W
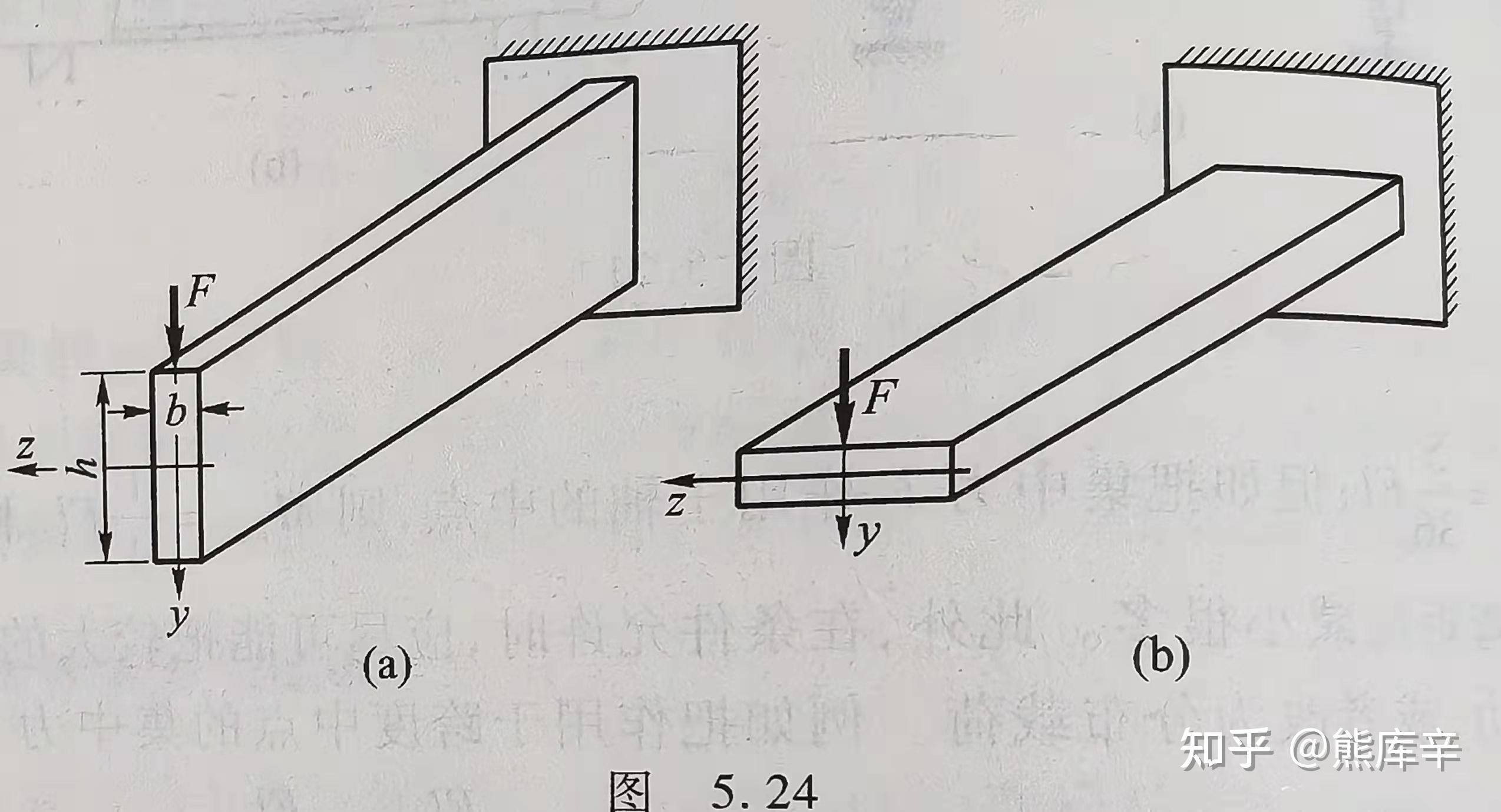
根据 M_{max}=σW 可知,弯矩M与抗弯截面系数W成正比,W越大越有利;通常来说截面面积越大,W越大;截面面积越小,W越大,则越经济;根据矩形截面抗弯截面系数 W=\frac{1}{6}bh^2 ,如下图所示,同样一根梁,竖放比横放抗弯能力更强;梁弯曲时离中性面越远的地方正应力越大,因此空心矩形截面比实心矩形截面更经济。
54、静矩、形心、轴惯性矩(求梁截面弯曲应力)、极惯性矩(求圆轴扭转截面切应力)、惯性积、惯性半径概念说明,请参考B站清华大学殷雅俊老师的材料力学公开课
第六章 弯曲变形
55、做了强度分析,确认结构不会发生破坏,为什么还要做刚度分析?
答:强度分析只能确认结构不会发生屈服、断裂等形式的破坏,但实际零件还对刚度(变形量)有要求,如果变形量过大,也无法正常工作。比如说变速器中的齿轮轴,若变形过大,会影响齿轮啮合,使磨损不匀,引发噪声,缩短寿命;此时即使材料仍处于弹性阶段,也看作已经失效。车门抗凹分析中,若车门表面覆盖件刚度太低,用户会认为汽车质量太差,影响用户体验。
56、挠度:横坐标为x的横截面的形心沿y方向的位移,即梁的变形量,向上的挠度为正,向下的挠度为负,下图中梁的挠度为负
截面转角:梁的横截面对其原来位置转过的角度,逆时针的转角为正,顺时针的转角为正,下图中梁的转角为负
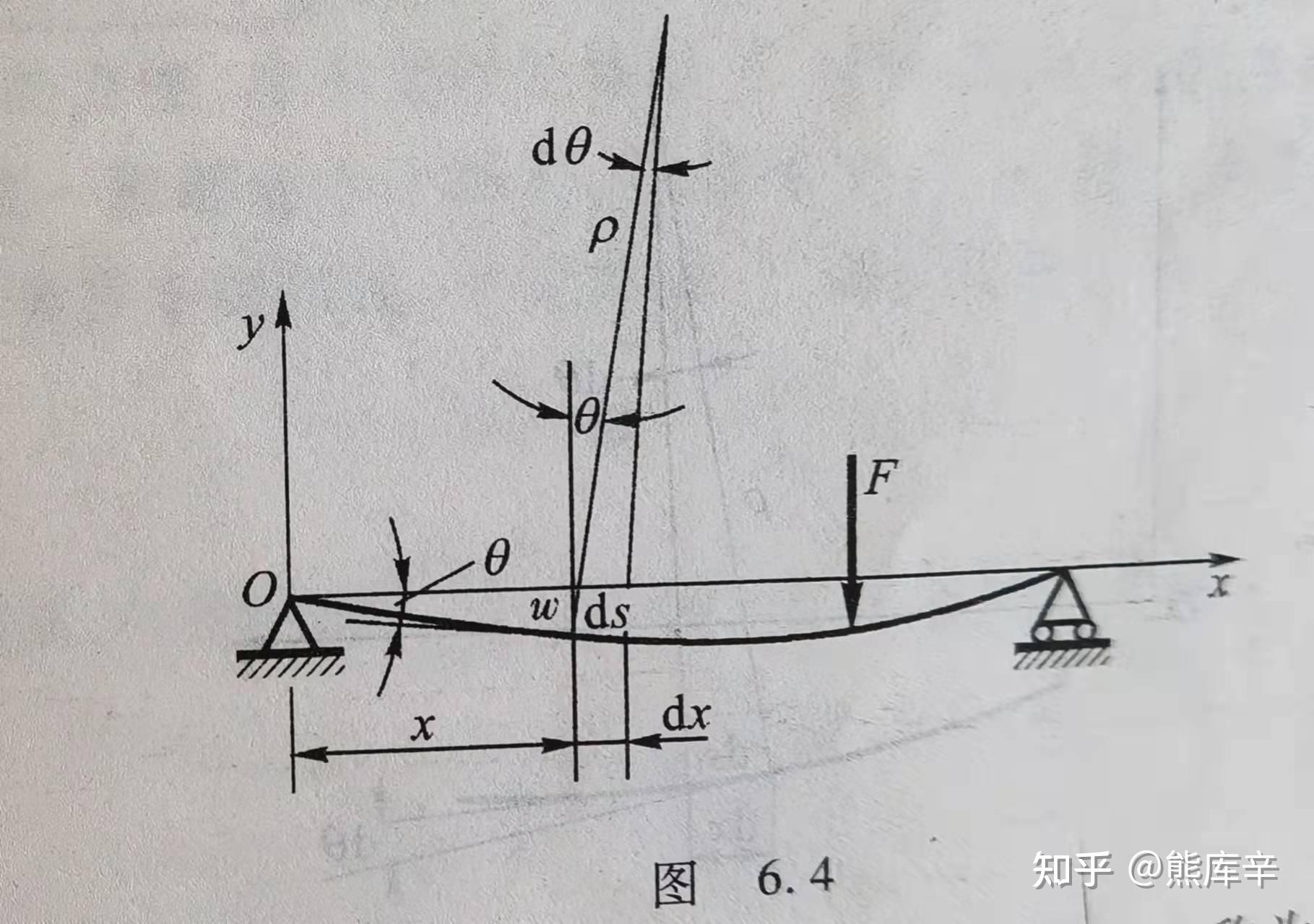
57、根据几何关系和第五章中的纯弯曲梁截面弯矩计算公式 \frac{1}{\rho}=\frac{M}{EI} ,可得到挠曲线的近似微分方程 \frac{d^2w}{dx^2}=\frac{M}{EI} ,根据相应的边界条件(比如固定约束等),积分进行求解
小变形情况下,梁的变形是线性的,不同载荷造成的梁的变形可以分开求解,然后再叠加;比如力F1和弯矩M2两个力分别加载时梁的最大变形为D1和D2,则F1和M2同时加载时梁的最大变形为D1+D2
58、如何减小弯曲变形?
- 改善结构形式和载荷作用方式,减小弯矩
- 弯矩是引起梁弯曲变形的主要因素,缩小跨度可有效减小载荷的力臂,从而减小弯矩
- 将集中力切换为均布载荷,相当于力臂减小,也能减小弯矩
- 选择合理的截面形状
- 相同截面积,但惯性矩不一定相等,工字梁、T形截面、槽形截面都比相同面积矩形截面有更大的惯性矩
第七章 应力和应变分析、强度理论
59、应力状态:围绕一点A取出一个正方体,在三个方向上尺寸均为无穷小(可用正方体的应力分布代表点A的应力情况),因此可以认为其每个平面上应力都是均匀分布的,正方体角度不同,每个平面上应力也不同;围绕A点取任意正方体每个面上的应力分布情况即应力状态
60、主平面:微元体某一表面上只有正应力,没有切应力,这种平面即主平面;
主应力:主平面上的正应力即为主应力;通过受力构件上任意一点都可以找到三个相互垂直的主平面,因此每个点都有三个主应力;
单向应力状态:三个主应力中只有一个不为零
平面应力状态:三个主应力中有两个不为零
空间应力状态:三个主应力都不为零
61、典型二向应力状态——薄壁圆筒(内径大于20倍壁厚)
薄壁圆筒主应力计算圆筒轴向mm截面上主应力为\sigma' = \frac{F}{A} = \frac{p*\frac{\pi D^2}{4}}{\pi D\delta}=\frac{pD}{4\delta}
圆筒沿轴线方向切割面mn上内力 =2\sigma''\delta l=plD= 压力, \sigma''=\frac{plD}{2\delta l}
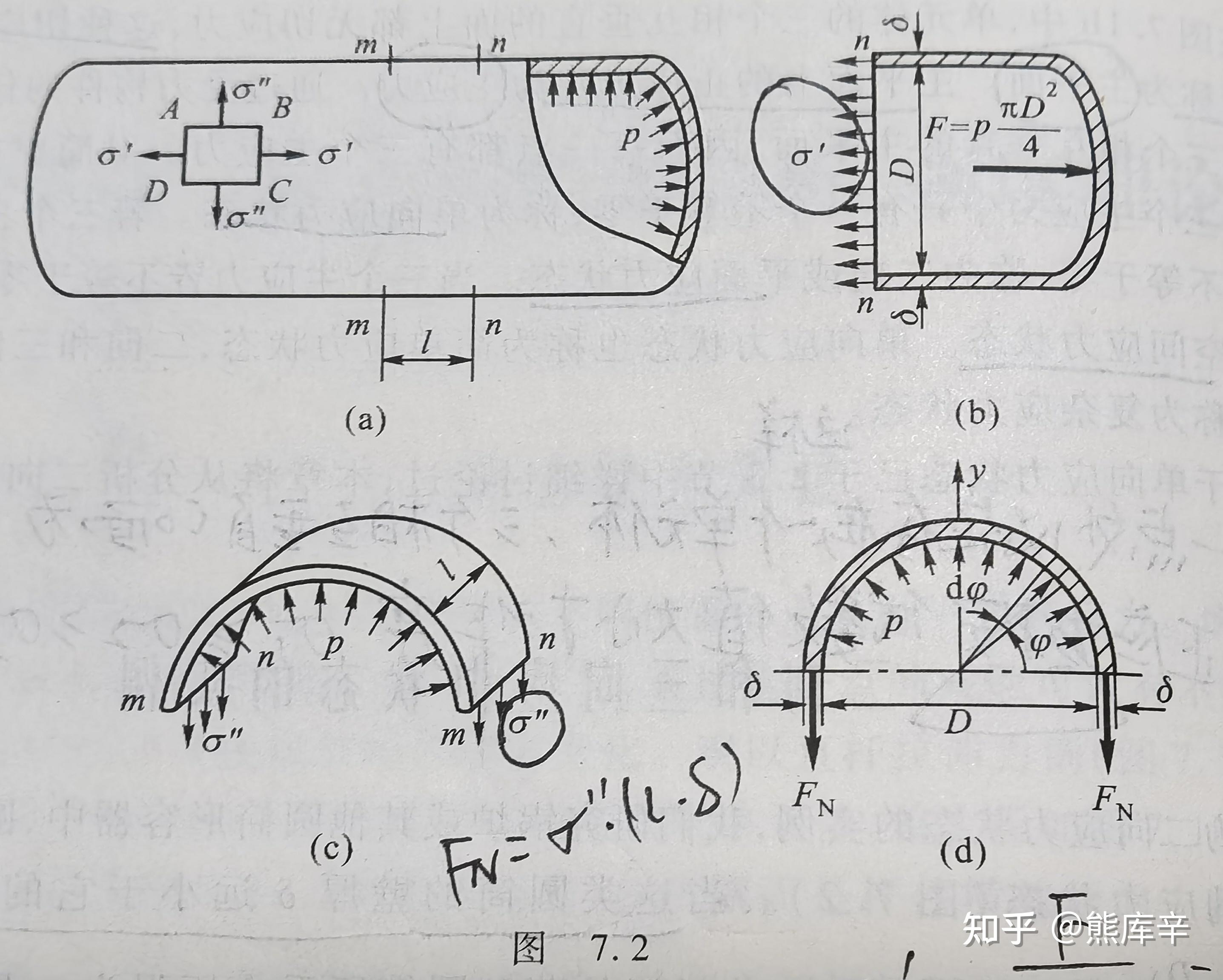
薄壁圆筒受力情况
典型三向应力状态——滚珠轴承中滚珠与外圈接触点处的应力状态
在滚珠与外圈的接触面上,有接触应力 \sigma_3 ;由于 \sigma_3 的作用,单元体将向周围膨胀,于是引起周围材料对他的约束应力 \sigma_1 和 \sigma_2 。
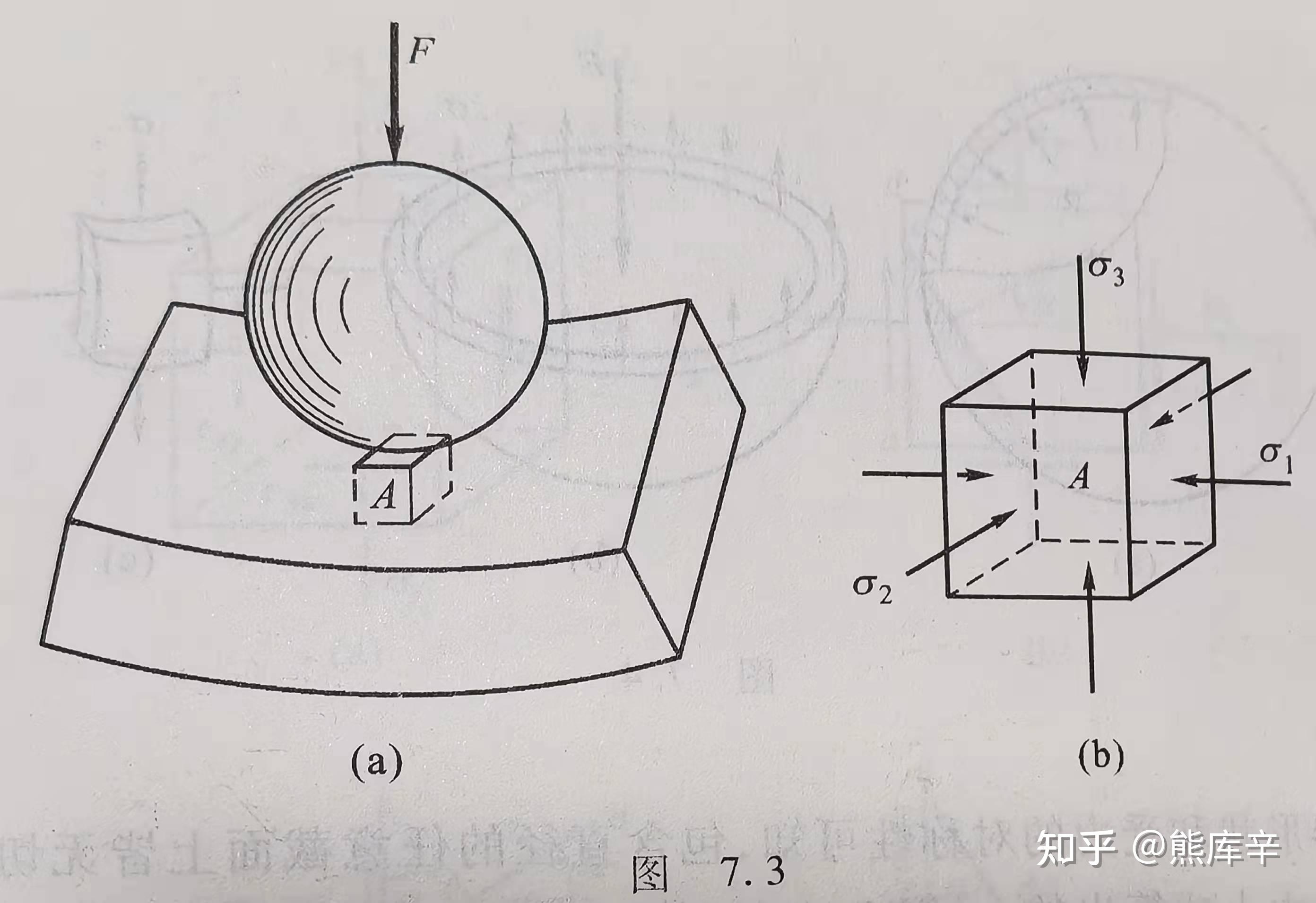
典型三向应力状态——滚珠挤压轴承外圈
62、应力下标规定: \tau_{xy}
第一个下标x表示切应力作用平面的法向方向,第二个下标表示y表示切应力的方向平等于y轴
应力正负号规定:
正应力:拉应力为正,压应力为负
切应力:切应力对单元体内任意点的矩为顺时针转向时,规定为正,反之为负
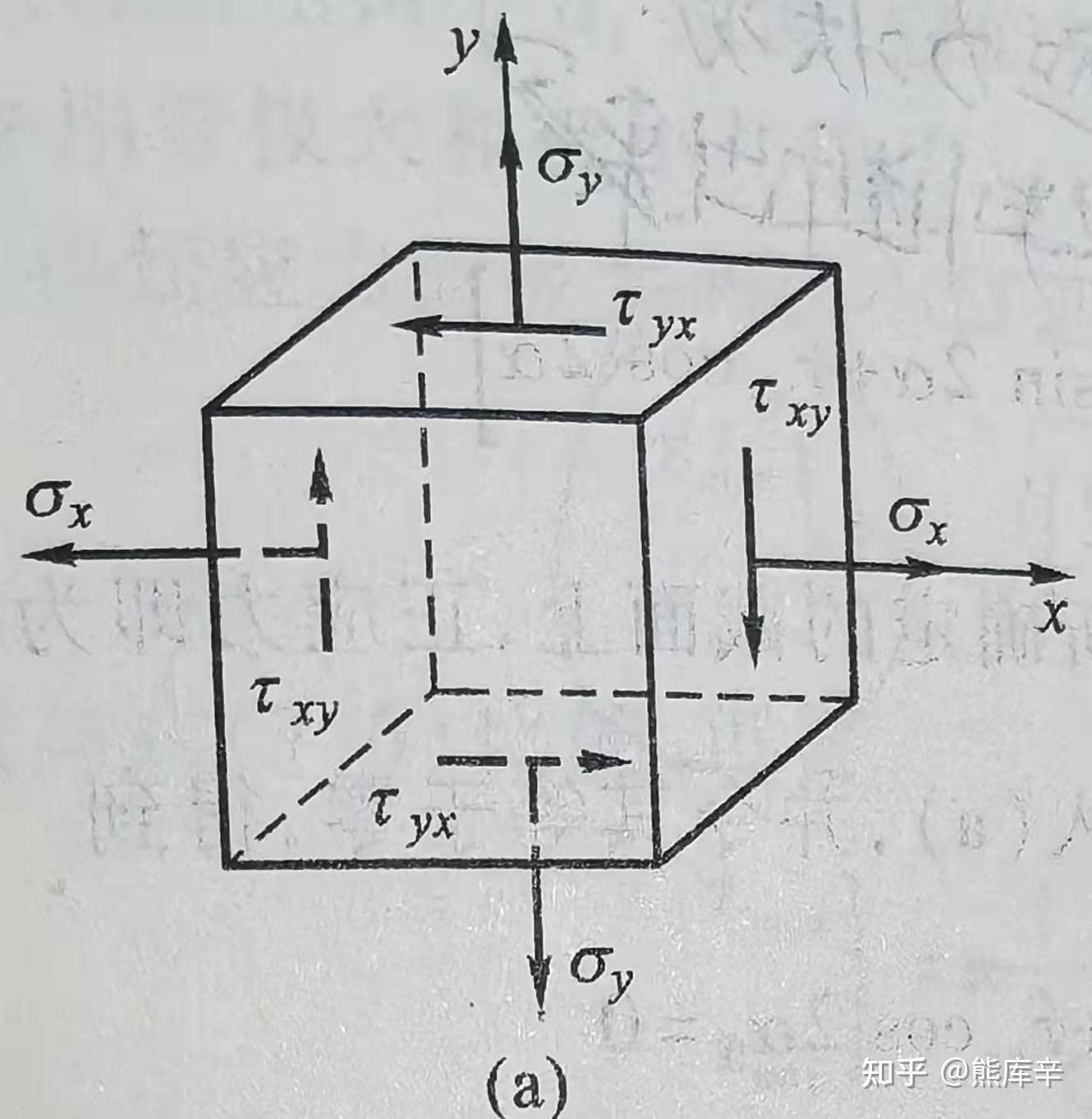
应力下标规定
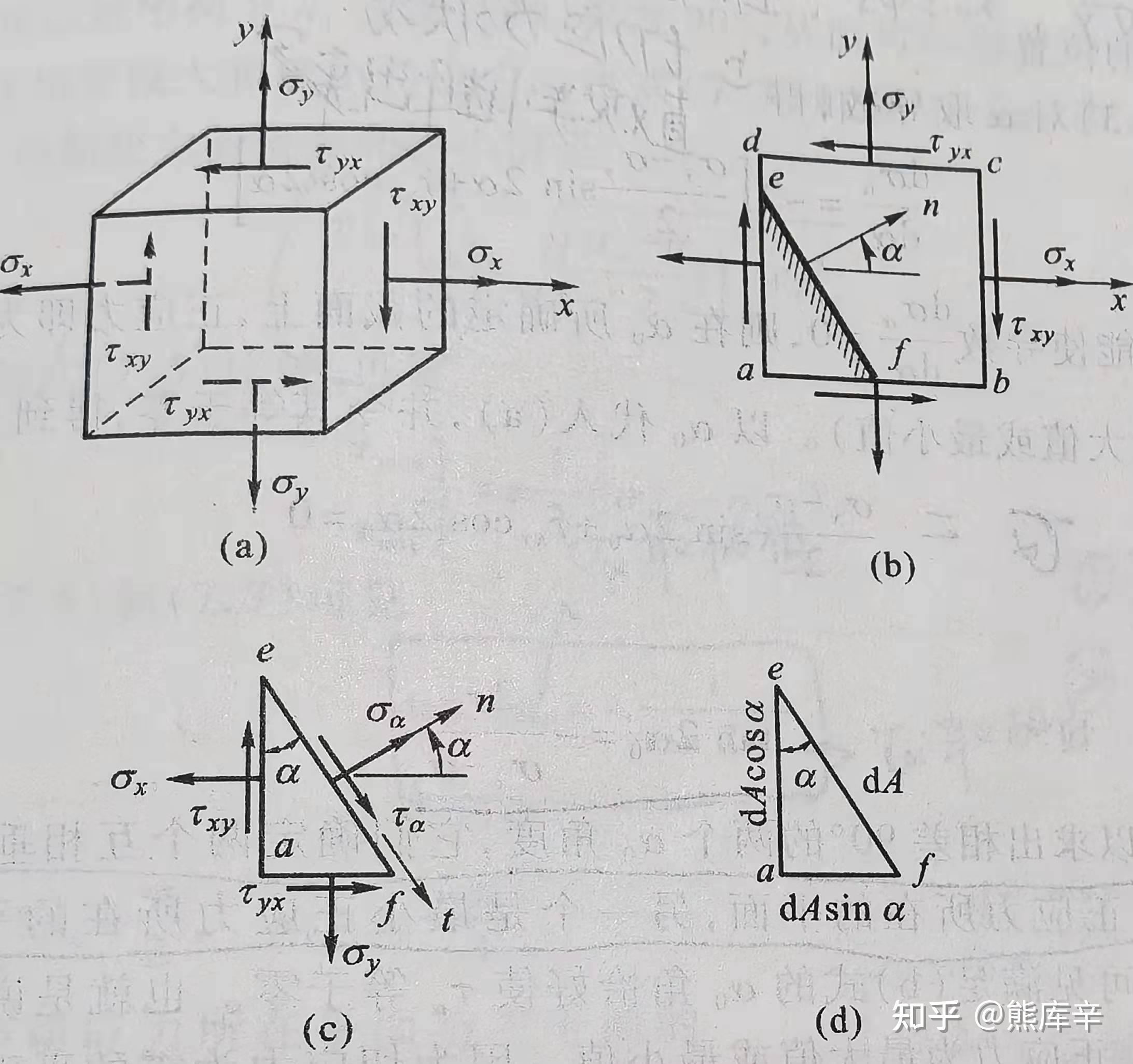
63、二向应力状态——解析法
已知通过一点的某些截面上的应力状态后,可以通过力平衡方程获得通过该点任间截面上的应力状态,确定主应力和主平面
根据下图(a)所示的应力状态,如何求解图(c)所示截面上的n方向正应力和t方向切应力?
沿n方向和t方向列两个力平衡方程,即可根据图(a)中的应力状态求解图(c)中的正应力和切应力
t方向切应力 \tau _{\alpha}=\frac{\sigma_x-\sigma_y}{2}sin2\alpha+\tau_{xy}cos2\alpha
n方向正应力 \sigma_\alpha=\frac{\sigma_x+\sigma_y}{2}+\frac{\sigma_x-\sigma_y}{2}cos2\alpha-\tau_{xy}sin2\alpha
n方向正应力计算公式对角度 \alpha 求导可得: \frac{d\sigma_\alpha}{d\alpha}=-2[\frac{\sigma_x-\sigma_y}{2}sin2\alpha+\tau_{xy}cos2\alpha]=-2\tau _{\alpha}
该导数取零时(切应力为零),主应力取最大值或最小值——即切应力等于零的平面上,正应力为最大值或最小值——即切应力为零的平面上,正应力取最大或最小值
最大/最小正应力计算公式: \sigma_{max}/\sigma_{min}=\frac{\sigma_x+\sigma_y}{2}\pm\sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau^2_{xy}}
最大/最小切应力计算公式: \tau_{max}/\tau_{min}=\pm\sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau^2_{xy}}
二向应力状态
评:有限元软件可以直接计算出主应力和切应力,工程师只需要知道如何计算即可,不需要真的手动计算;手动计算可用于验证有限元计算结果准确性的依据。
64、二向应力状态——图解法
应力圆推导过程
二向应力状态——图解法 根据解析法中的任意角度正应力和切应力计算公式,移项可得如下等式:
\sigma_\alpha-\frac{\sigma_x+\sigma_y}{2}=\frac{\sigma_x-\sigma_y}{2}cos2\alpha-\tau_{xy}sin2\alpha
\tau _{\alpha}=\frac{\sigma_x-\sigma_y}{2}sin2\alpha+\tau_{xy}cos2\alpha
两个等式左右两侧同时平方,即可消去角度α,得到一个以正应力 \sigma_\alpha 和切应力 \tau_\alpha 为变量的圆的方程,圆心为( \sigma_\alpha ,0),半径为 \frac{\sigma_x+\sigma_y}{2} ,方程如下:
(\sigma_\alpha-\frac{\sigma_x+\sigma_y}{2})^2+\tau^2_\alpha=(\frac{\sigma_x-\sigma_y}{2})^2+\tau^2_{xy}
应力圆作图过程
以 \sigma_x 为横坐标,以 \tau_{xy} 为纵坐标,根据图(a)中的正应力\sigma_\alpha和切应力\tau_\alpha确定D点和D'点的坐标,DD'中点C即圆心
D点坐标:(\sigma_x,\tau_{xy})
D'点坐标:( \sigma_y , -\tau_{xy} )
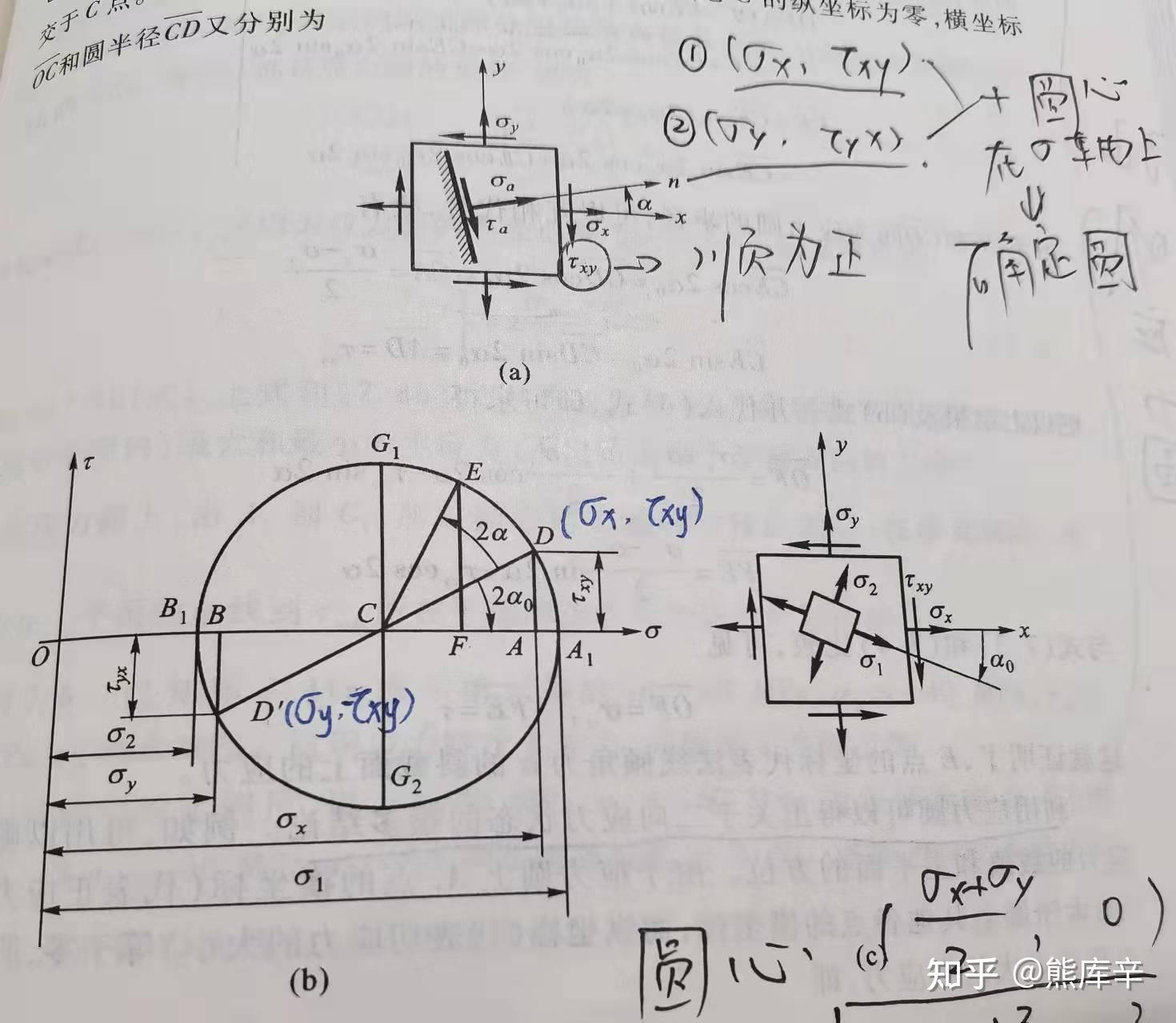
根据应力圆,可以快速确定最大/最小正应力,切应力
最大正应力点A1横坐标,最小正应力点B1横坐标;
最大切应力:G1和G2点纵坐标
65、三向应力状态
已知过某点单元体上的三个主应力时,如下图所示,可以求解该单元体上任意斜截面上的正应力和切应力
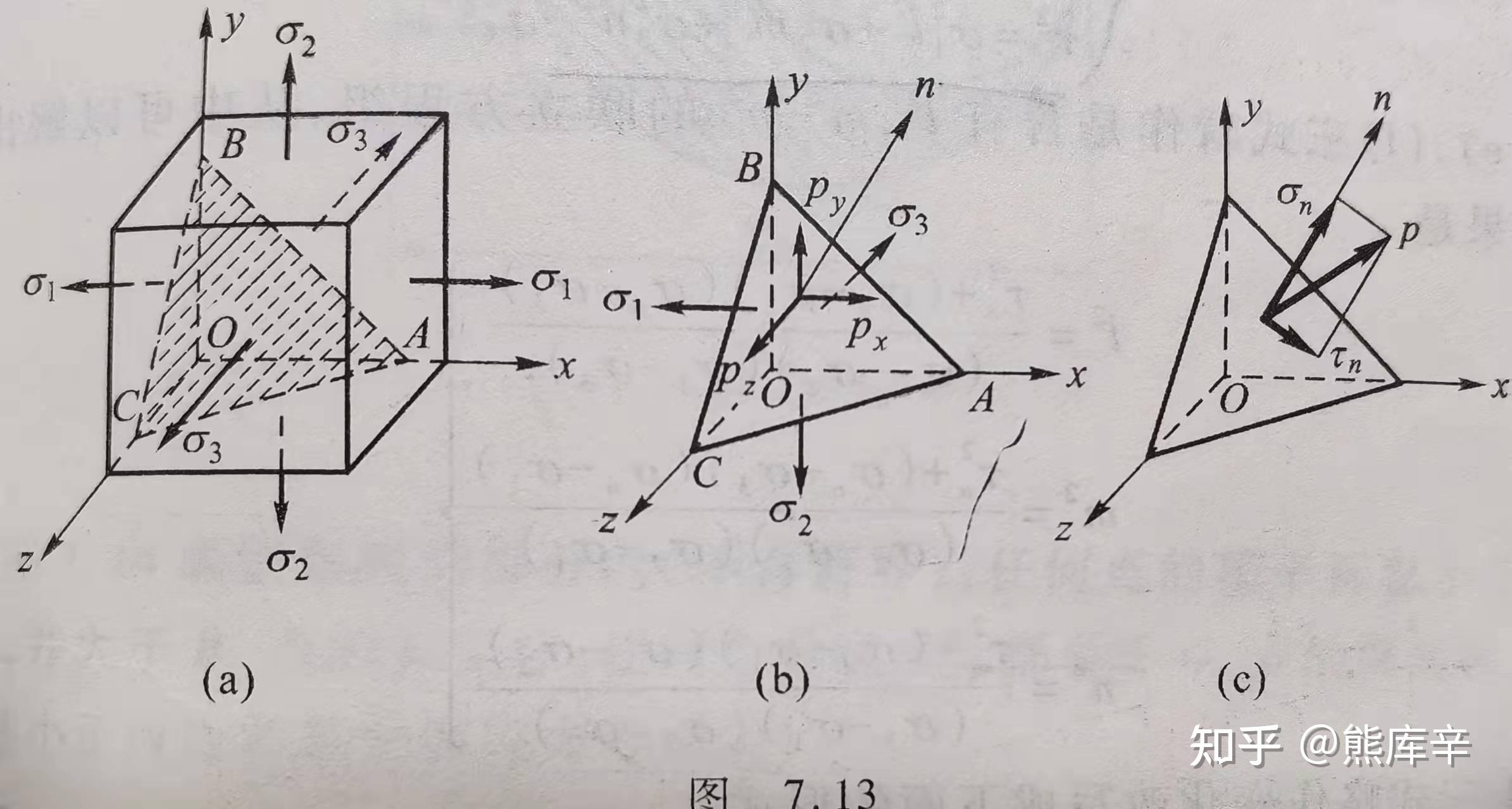
三向应力状态示意图
设斜截面上正应力为σn,切应力为τn;根据xyz三个方向的力平衡方程,可以得出如下所示三个圆的方程,其中l、m和n是方向余弦
(\sigma_n-\frac{\sigma_2+\sigma_3}{2})^2+\tau^2_n=(\frac{\sigma_2-\sigma_3}{2})^2+l^2(\sigma_1-\sigma_2)(\sigma_1-\sigma_3)\geq(\frac{\sigma_2-\sigma_3}{2})^2
(\sigma_n-\frac{\sigma_3+\sigma_1}{2})^2+\tau^2_n=(\frac{\sigma_3-\sigma_1}{2})^2+m^2(\sigma_2-\sigma_3)(\sigma_2-\sigma_1)\leq(\frac{\sigma_3-\sigma_1}{2})^2
(\sigma_n-\frac{\sigma_1+\sigma_2}{2})^2+\tau^2_n=(\frac{\sigma_1-\sigma_2}{2})^2+n^2(\sigma_3-\sigma_1)(\sigma_3-\sigma_2)\geq(\frac{\sigma_1-\sigma_2}{2})^2
根据上述三个方程,可以画出如下所示三个圆,阴影部分即为任意斜截面上的正应力和切应力;由应力圆可知,最大正应力为 \sigma_1 和 \sigma_3 和,最大切应力为 \frac{\sigma_1-\sigma_3}{2}
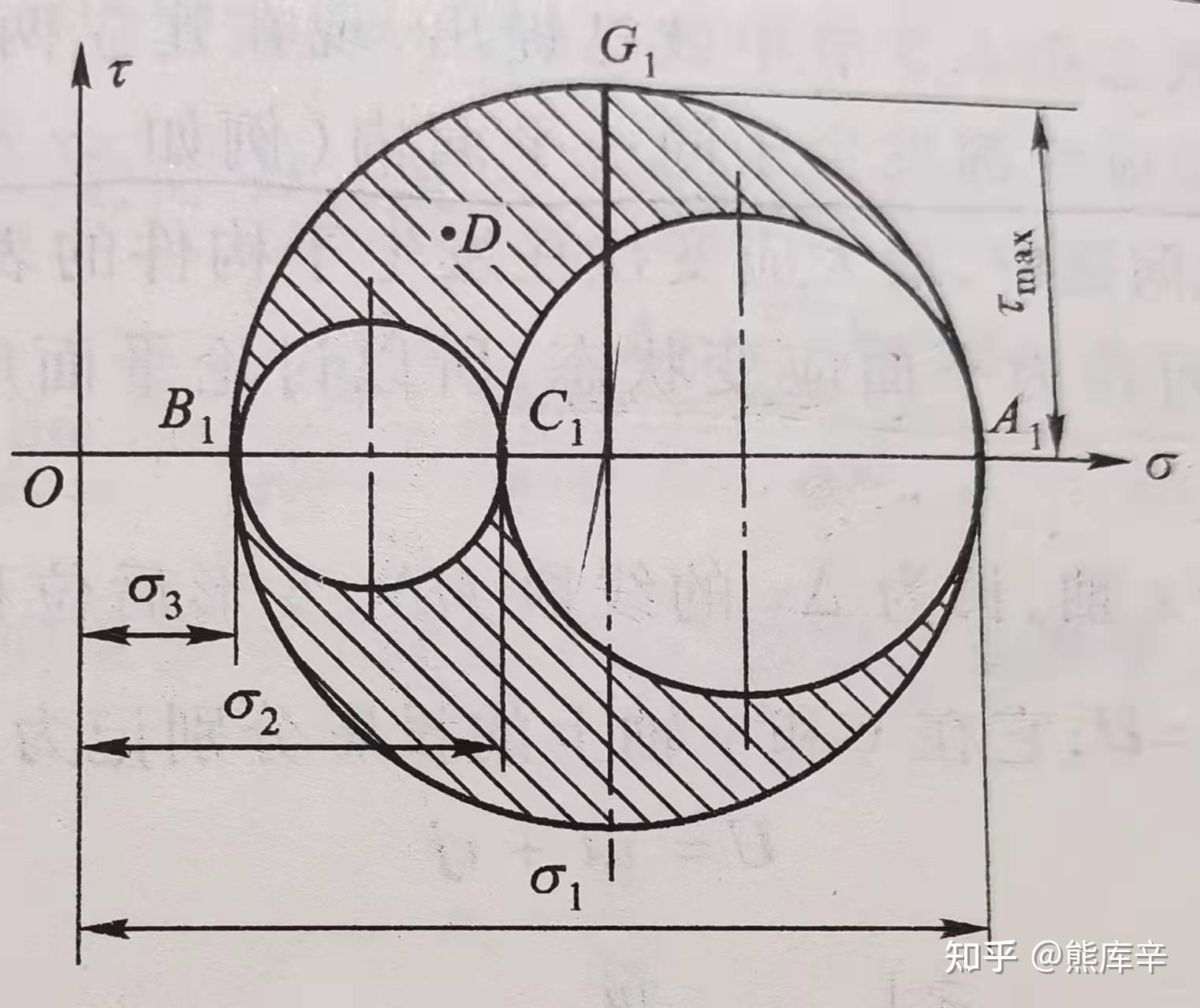
三向应力状态-图解法
66、广义胡克定律
前提条件:各向同性线弹性材料+小变形,小变形线弹性范围内,线应变只与正应力有关,与切应力无关;切应变只与切应力有关,而与正应力无关
定律说明:最普遍的情况下,描述一点的应力状态需要如下图所示的9个应力分量,每个面内一个正应力,两个切应力,考虑切应力互等定理, τ_{xy}=τ_{yx},τ_{yz}=τ_{zy},τ_{xz}=τ_{zx} ,原来的9个应力分量中只有6个是独立的,其关系可用如下6个等式表示,即广义胡克定律
\varepsilon_{x} = \frac{1}{E}[\sigma_{x}-\mu(\sigma_{y}+\sigma_{z})]
\varepsilon_{y} = \frac{1}{E}[\sigma_{y}-\mu(\sigma_{x}+\sigma_{z})]
\varepsilon_{z} = \frac{1}{E}[\sigma_{z}-\mu(\sigma_{x}+\sigma_{y})]
\gamma_{xy}=\frac{\tau_{xy}}{G}, \gamma_{yz}=\frac{\tau_{yz}}{G}, \gamma_{zx}=\frac{\tau_{zx}}{G}
当单元体的六个主面皆为主平面时,只有正应力,没有切应力,广义胡克定律转化为
\varepsilon_{1} = \frac{1}{E}[\sigma_{1}-\mu(\sigma_{2}+\sigma_{3})]
\varepsilon_{2} = \frac{1}{E}[\sigma_{2}-\mu(\sigma_{1}+\sigma_{3})]
\varepsilon_{3} = \frac{1}{E}[\sigma_{3}-\mu(\sigma_{1}+\sigma_{2})]
\gamma_{xy}=0, \gamma_{yz}=0, \gamma_{zx}=0
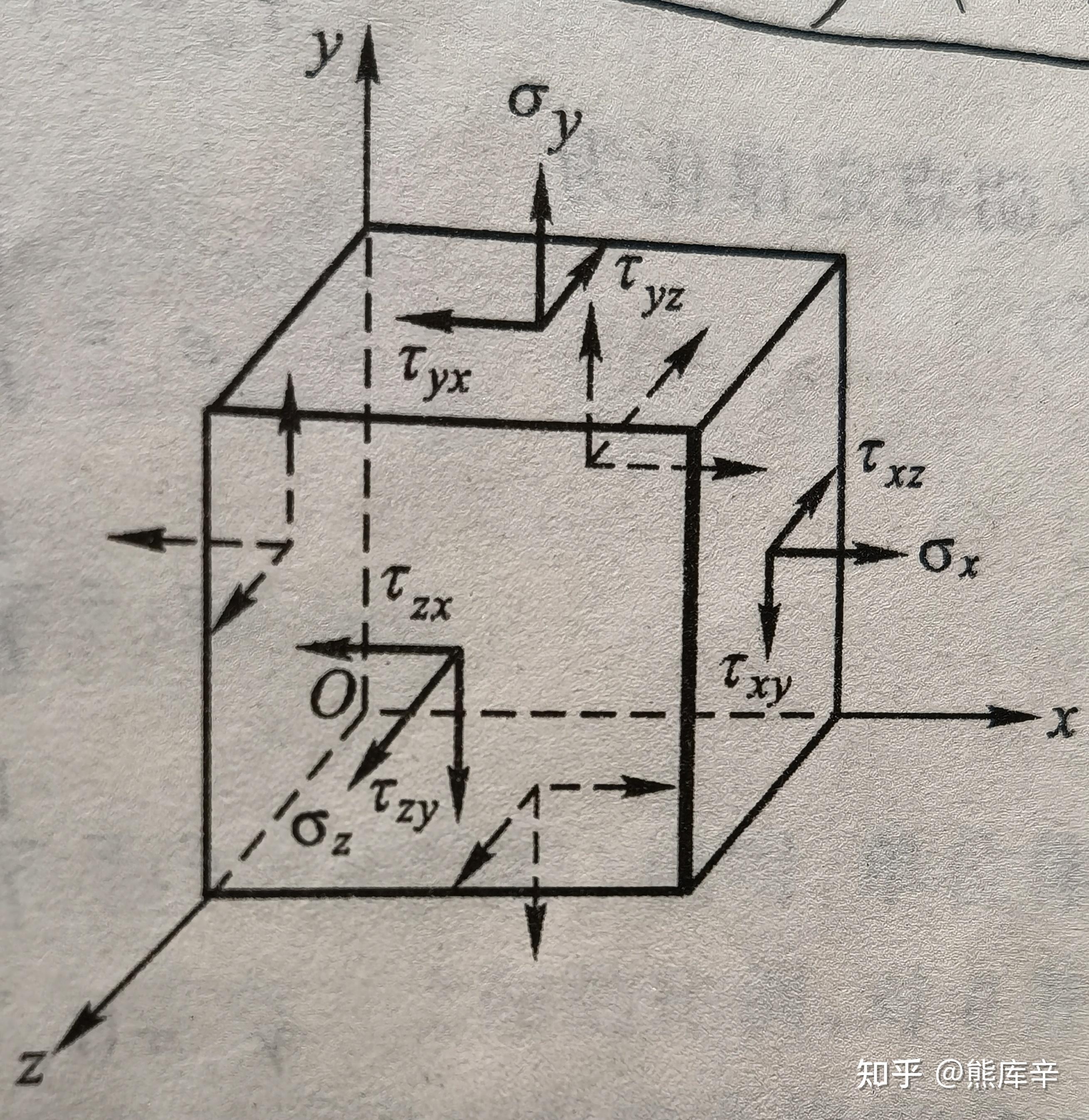
一点应力状态
体积胡克定律:体积变化量和应力间的关系
变形前:单元体边长为dx,dy,dz,体积为 V=dxdydz
变形后:单元体边长为
dx+\epsilon_1dx=(1+\epsilon_1)dx
dy+\epsilon_2dy=(1+\epsilon_2)dy
dz+\epsilon_3dz=(1+\epsilon_3)dz
单元体体积计算公式如下,最后一个约等于符号表示右侧已略去高阶小项
V_1 = (1+\epsilon_1)(1+\epsilon_2)(1+\epsilon_3)dxdydz\approx(1+\epsilon_1+\epsilon_2+\epsilon_3)dxdydz
单位体积的体积改变量,即体积胡克定律表达式为:
\theta=\frac{V_{1}-V}{V}=\epsilon_1+\epsilon_2+\epsilon_3 ,将广义胡克定律代入上式得体积胡克定律表达式
\theta=\epsilon_1+\epsilon_2+\epsilon_3=\frac{1-2\mu}{E}(\sigma_1+\sigma_2+\sigma_3)=\frac{3(1-2\mu)}{E}*\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}}{3}=\frac{\sigma_{m}}{K} ,
其中K=\frac{E}{3(1-2\mu)} 为体积弹性模量, \sigma_m = \frac{\sigma_1+\sigma_2+\sigma_3}{3} 为三个主应力平均值。
根据体积胡克定律表达式,体积改变量只与三个主应力之和有关,与三个主应力间具体比例无关,某些情况下,为计算简便,可取三个应力大小相等;体积弹性模量K一定取正值,因此1−2μ大于零,μ小于0.5。
67、复杂应力状态下的应变能密度
单向拉伸或压缩时,应变能密度计算公式如下: \upsilon_\epsilon=\frac{1}{2}\sigma\epsilon
三向应力状态下,三个主应力分别产生应变能(简单起见,只考虑主应力状态,不考虑存在切应力的状态)
\upsilon_\epsilon=\frac{1}{2}\sigma_1\epsilon_1+\frac{1}{2}\sigma_2\epsilon_2+\frac{1}{2}\sigma_3\epsilon_3=\frac{1}{2E}[\sigma^2_1+\sigma^2_2+\sigma^2_3-2\mu(\sigma_1\sigma_2+\sigma_2\sigma_3+\sigma_3\sigma_1)]
\upsilon_\epsilon=\upsilon_v+\upsilon_d
若变形前单元体为正方体,只考虑主应力的情况下,单元体将由正方体变形为长方体,变形能量可分为两部分,即 V_ϵ=V_v+V_d
- 因体积变化而储存的体积改变应变能密度 V_v
- 体积不变,但由正方体改变为长方体而储存的应变能密度 V_d ,称为畸变能密度
根据体应变计算公式,体应变与分别施加三个主应力时相等,但此时三条棱边变形相同,单元体只有体积变化,没有形状变化,此时只存在体积应变能密度 V_v 。
若在单元体上以平均应力代替三个主应力 \sigma_m=\frac{\sigma_1+\sigma_2+\sigma_3}{3} ,根据体应变计算公式,体应变与分别施加三个主应力时相等,但此时三条棱边变形相同,单元体只有体积变化,没有形状变化,此时只存在体积应变能密度 \upsilon_v=\frac{1}{2}\sigma_m\epsilon_m+\frac{1}{2}\sigma_m\epsilon_m+\frac{1}{2}\sigma_m\epsilon_m=\frac{3}{2}\sigma_m\epsilon_m ;
将广义胡克定律计算公式 \epsilon_m=\frac{\sigma_m}{E}-\mu(\frac{\sigma_m}{E}+\frac{\sigma_m}{E})=\frac{(1-2\mu)}{E}\sigma_m 代入上述体积应变能密度计算公式得: \upsilon_v=\frac{3(1-2\mu)}{2E}\sigma^2_m=\frac{1-2\mu}{6E}(\sigma_1+\sigma_2+\sigma_3)^2
应变能密度减去体积应变能密度,可得畸变能密度计算公式: \upsilon_d=\frac{1+\mu}{6E}[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2]
杨氏模量、泊松比和剪切模量关系推导:由两种纯剪切工况应变能密度方法得到的应变能密度相等,进行推导。
具体推导过程如下:
纯剪切应变能密度计算方法1:
纯剪切时,扭转截面上只有切应力,没有正应力,因此应变能密度可等效为: \upsilon_\epsilon=\frac{1}{2}\tau\gamma=\frac{1}{2}\tau\frac{\tau}{G}=\frac{\tau^2}{2G}
纯剪切应变能密度计算方法2:
纯剪切应力状态为: \sigma_x=\sigma_y=0, \tau_{xy}=\tau
根据解析法,可由过某点任一截面的应力状态计算主应力,纯剪切工况下,最大最小主应力计算公式为:
\sigma_{max}/\sigma_{min}=\frac{\sigma_x+\sigma_y}{2}\pm\sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau^2_{xy}}=\pm\tau
代入三向应力状态下,应变能密度计算公式: \upsilon_\epsilon=\frac{1}{2}\sigma_1\epsilon_1+\frac{1}{2}\sigma_2\epsilon_2+\frac{1}{2}\sigma_3\epsilon_3=\frac{1}{2E}[\sigma^2_1+\sigma^2_2+\sigma^2_3-2\mu(\sigma_1\sigma_2+\sigma_2\sigma_3+\sigma_3\sigma_1)]=\frac{\tau^2(1+\mu)}{E}
纯剪切工况下,两种方法计算得到的应变能密度相同,可得等式: \upsilon_\epsilon=\frac{\tau^2}{2G}=\frac{\tau^2(1+\mu)}{E}
变换可得杨氏模量、剪切模量和泊松比间关系 G=\frac{E}{2(1+\mu)} 。
到此,杨氏模量、泊松比和剪切模量三者关系证明完毕。
68、强度理论概述
如何判断材料是否失效是材料力学的重要任务,前面所介绍的拉压、弯曲、扭转和剪切变形等所有内容都是为失效准则作铺垫的,结构强度有限元分析的最终目的也是想知道结构是否会失效;
- 屈服和断裂是两种常见的失效方式,塑性材料应力达到屈服极限时发生塑性屈服失效,脆性材料应力达到强度极限时发生断裂失效;
- 单向应力状态下,可通过拉伸实验得到材料的屈服极限和强度极限,作为材料是否发生失效的判断依据
- 实际构件危险点的应力状态往往不是单向的,通常是二向或者三向复杂应力状态,很难通过实验全部复现
问题:如何根据简单应力状态下的实验结果,来判断复杂应力状态下材料是否发生失效?
答:通过经验总结,提出各种假说,认为应力、应变或应变能密度是引起失效的主要原因,这些假说即强度理论;
根据这些强度理论,便可由简单应力状态下的实验结果,来判断复杂应力状态下,材料是否会发生失效;
经过大量的实践证明,畸变能密度理论适用于铁、铜、铝等塑性材料失效判断依据,最大拉应力理论适用于铸铁、石料、混凝土和玻璃等塑性材料失效判断依据
问:如何用实验模拟单向、二向应力状态?
答:拉压实验可模拟单向应力状态;
薄壁圆筒在内压力作用下,圆筒壁为二向应力状态;如果再加上轴向拉力,可使两个主应力之比等于各种预定值;如果再加上扭转力偶,可以得到更普遍的受力情况;
69、四种常用强度理论
解释断裂失效:
- 最大拉应力理论:
- 最大拉应力是引起断裂的主要因素,无论什么应力状态,只要最大拉应力达到材料强度极限,材料发生断裂失效;
- 最大拉应力的极限值与材料性能无关,因此可用单向拉伸实验的强度极限来确定该极限值;
- 适用于铸铁等脆性材料
- 不适用于没有拉应力的状态,如单向压缩、三向压缩等
- 最大伸长线应变理论:
- 最大伸长线应变是引起断裂的主要因素,无论什么应力状态,只要最大伸长线应变达到与材料性能相关的某一极限,材料即发生断裂;
- 最大伸长线应变与应力状态无关,可用单向拉伸实验来确定,根据胡克定律,可将应变转换为应力用于失效判断,判断公式如下: \epsilon_1=\frac{1}{E}[\sigma_1-\mu(\sigma_2+\sigma_3)]\leq\epsilon_{max} ,转换为应力判断公式为\sigma_1-\mu(\sigma_2+\sigma_3)\leq[\sigma]
解释屈服失效:
- 最大切应力理论——1864年,法国工程师Tresca提出
- 最大切应力是引起屈服的主要因素,无论什么应力状态,只要最大切应力达到与材料性能有关的某一极限值,材料就发生屈服;
- 最大切应力极限值与应力状态无关,因此可用单向拉伸实验来确定切应力极限值,意向拉伸时,与轴线45度的斜截面上切应力 \tau_{max}=\frac{\sigma_s}{2} 最大,因此屈服准则为切应力小于与轴线45度的斜截面上的切应力,即小于屈服极限应力的一半;由三向应力状态应力圆可知,任意应力状态下最大切应力为 \tau_{max}=\frac{\sigma_1-\sigma_3}{2} ,由此可得屈服准则为 \sigma_1-\sigma_3\leq\sigma_s ,对应有限元后处理结果中的Tresca Stress(第一主应力减第三主应力,不是剪应力)
- 相比畸变能密度理论,最大切应力理论偏保安全,纯剪切工况下,最大切应力理论算出来的等效应力比畸变能密度理论算出来的米塞斯应力大15%左右,压力容器校核多用最大切应力理论,相比畸变能密度理论更安全
- 畸变能密度理论——1913年由奥地利物理学家冯.米塞斯提出
- 畸变能密度是引起屈服的主要因素,无论什么应力状态,只要最大畸变能密度达到与材料性能有关的某一因素(通常用米塞斯应力来判断),材料即发生屈服;
- 综合考虑三个主应力的影响,无论什么应力状态,只要米塞斯应力达到某一极限值,材料就发生屈服;因此可用单向拉伸实验来确定米塞斯应力极限。
- 冯米塞斯应力计算公式: \sqrt{\frac{1}{2}[(\sigma_1-\sigma_2)^2_+(\sigma_2-\sigma_3)^2_+(\sigma_3-\sigma_1)^2_]}\leq\sigma_s ,对应有限元后处理软件中的Von Mises Stress
注意事项:
同种材料在不同应力状态下,可能有不同的失效形式
- 碳钢制成的螺钉受拉时,螺纹根部因应力集中引起三向拉伸,就会因断裂而破坏;因为当三向拉伸的三个主应力数值接近时,由第三或第四强度理论计算出的等效应力很小,不会屈服;
- 用淬火钢球压在铸铁板上,接触点附近的材料处于三向受压状态,随着压力增大,铸铁板会出现明显的凹坑,表明此时铸铁已发生屈服;
- 无论塑性或脆性材料,在三向拉应力相近的情况下,都将以断裂的形式失效,宜采用最大拉应力理论;在三向压应力相近的情况下,都可以引起塑性变形,宜采用第三或第四强度理论。
第八章 组合变形
70、组合变形问题——线性组合变形问题可用叠加原理进行求解
叠加原理:内力、应力、应变和位移等与外力成线性关系时,可分别计算每一基本变形各自引起的内力、应力、应变和位移,然后将所得结果叠加,便是构件在组合变形下的内力、应力、应变和位移;
71、截面核心问题——用有限元软件验证截面核心——圆柱体和长方体截面核心问题
任意截面形状的构件,若底部固定,在顶端截面上某点施加压力,存在一个环绕截面形心的区域,当压力作用于这一封闭区域内时,构件任一截面上只有压应力,没有拉应力,这个封闭区域称为截面核心。
截面核心意义:砖、石或混凝土短柱,抗压能力强抗拉能力弱,通常会要求横截面上不产生拉应力。
矩形截面核心:菱形阴影区域,边长分别为h/6和b/6
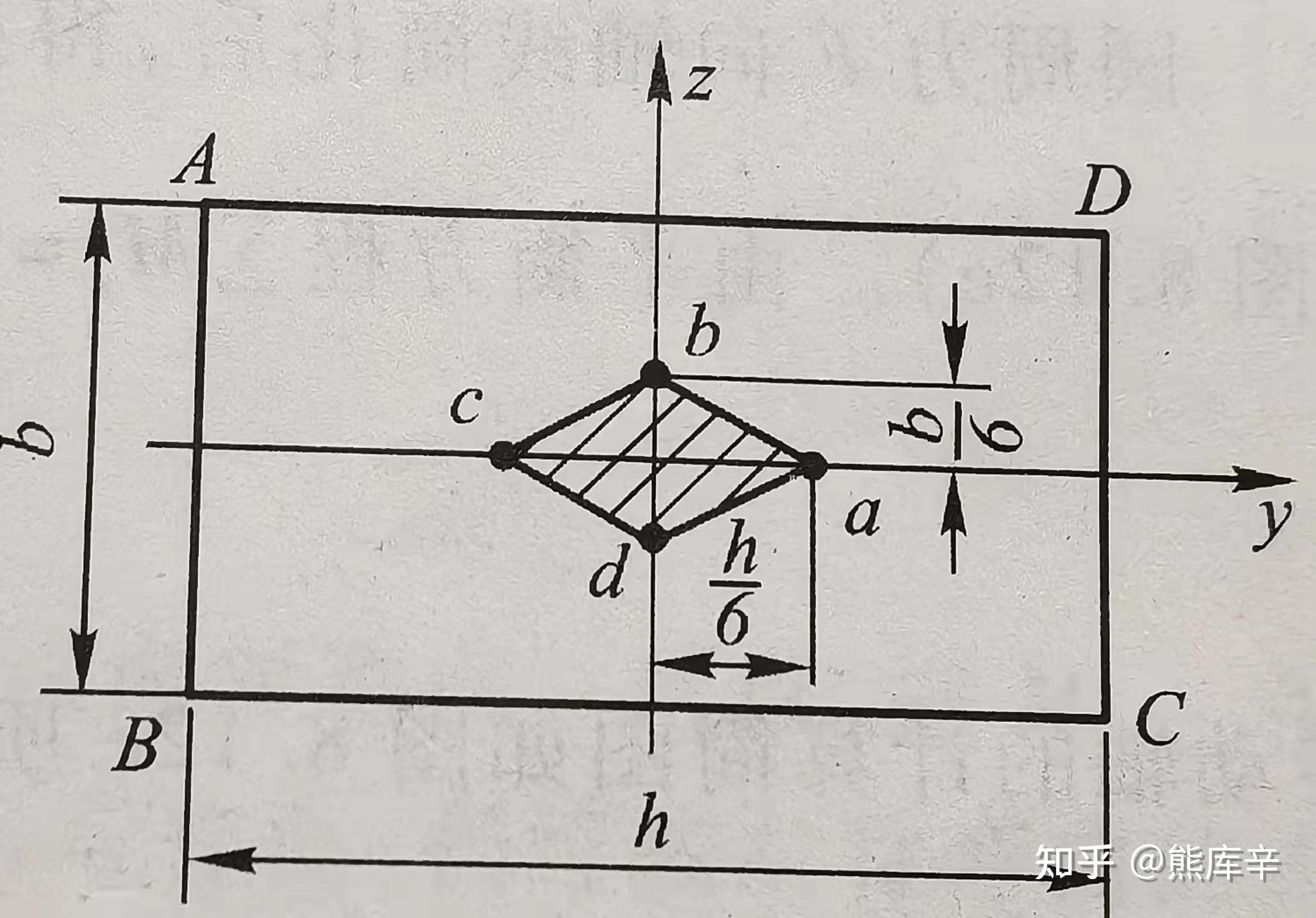
矩形截面核心
圆形截面核心:圆形阴影区域,半径为r/4,即截面半径的四分之一
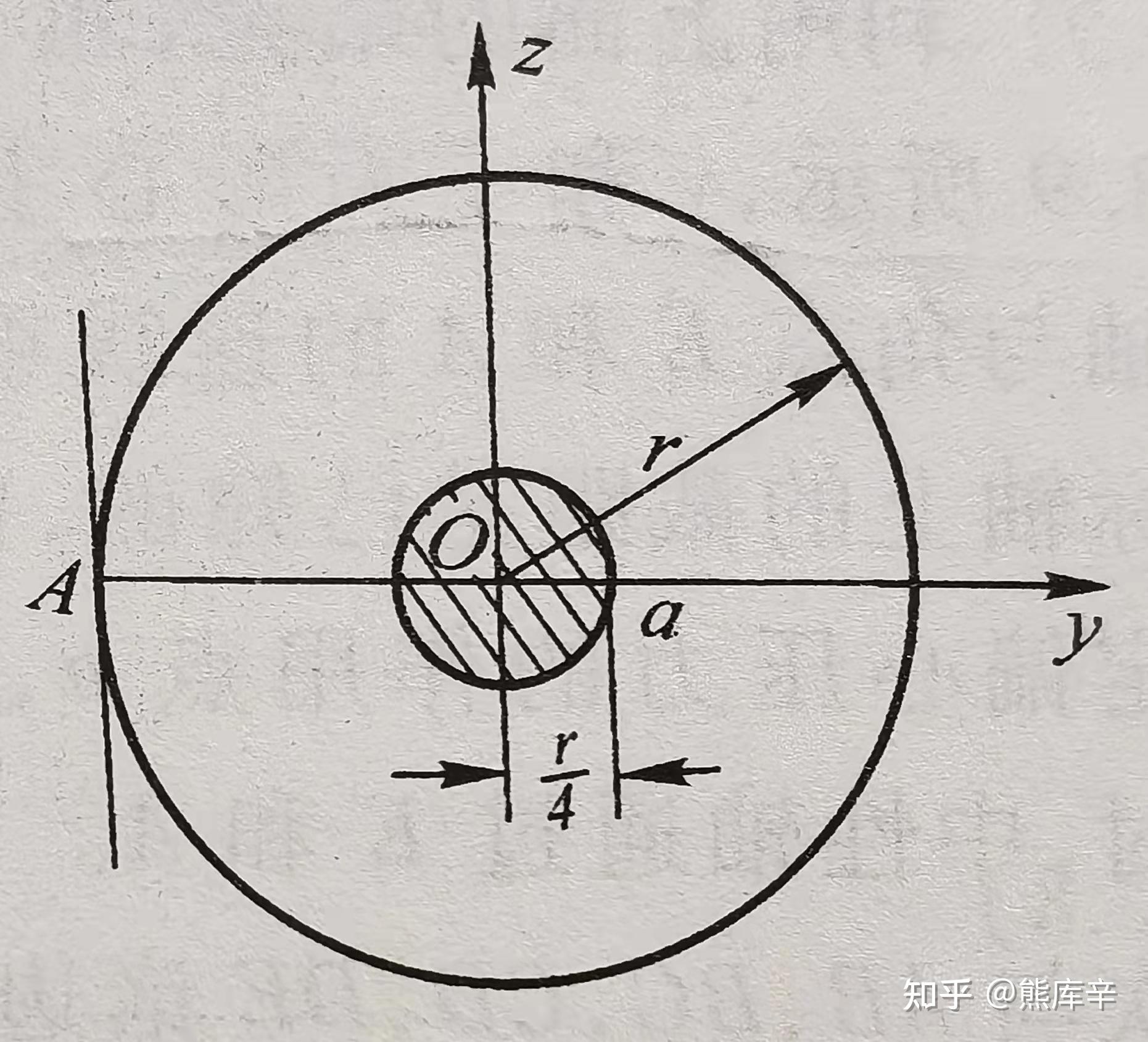
圆形截面核心
有限元验证
左侧模型在圆心处施加40N的压力,整个模型只有Z轴负方向变形,说明所有截面都处于被压缩状态;右侧模型在远离截面核心区域施加40N的压力,整个模型左侧有Z轴正向变形,右侧为Z轴负向变形,说明截面上存在拉应力。

有限元方法验证圆形截面核心问题
第九章 压杆稳定
72、如下图所示的两端铰支的细长杆,当杆两端受到与轴线重合的压力F时,F小于某一临界值Fr时,杆只受压,保持直线状态;当F等于某临界值Fr时,此时如果在杆侧向施加微小干扰,杆就会变弯,且当干扰解除后,杆依然保持曲线形状。临界值Fr称为临界压力或临界力,压杆丧失其直线形状的平衡而过渡为曲线平衡,称为丧失稳定性,简称失稳,也称为屈曲。
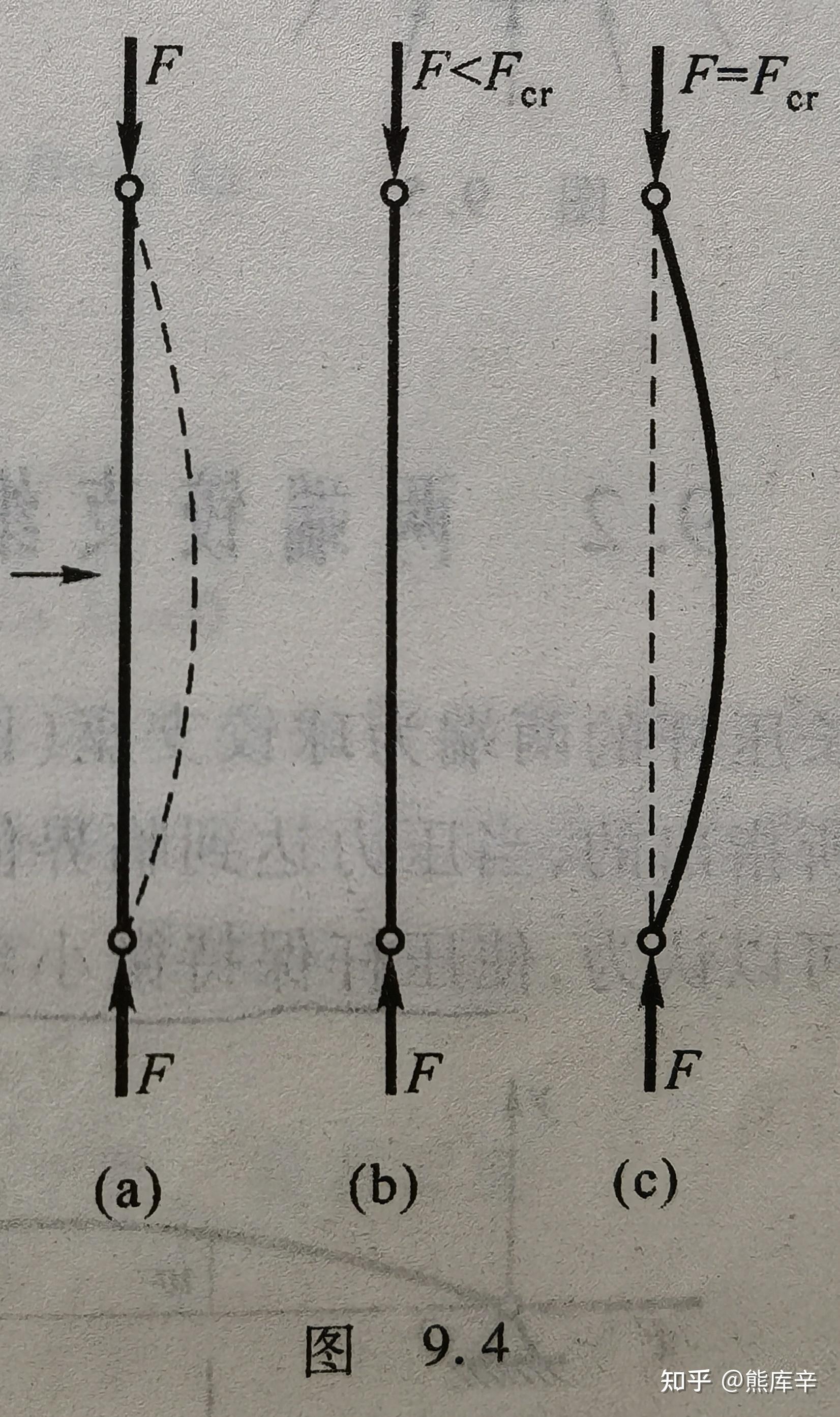
压杆失稳
杆件失稳后,压力的微小增加将引起弯曲变形的显著增大,杆件丧失承载能力,可能会导致机器无法正常工作;此时杆件上应力可能远低于强度极限,杆件无法正常工作并非因为强度不够,而是稳定性不够。
其他稳定性问题:
- 圆柱形薄壳在均匀外压作用下,壁内应力变为压应力,当外界压力达到临界值时,薄壳的圆形平衡就变为不稳定,会突然变成由虚线表示的椭圆形;
- 高度明显大于宽度的梁也可能发生侧向弯曲和扭转,发生失稳
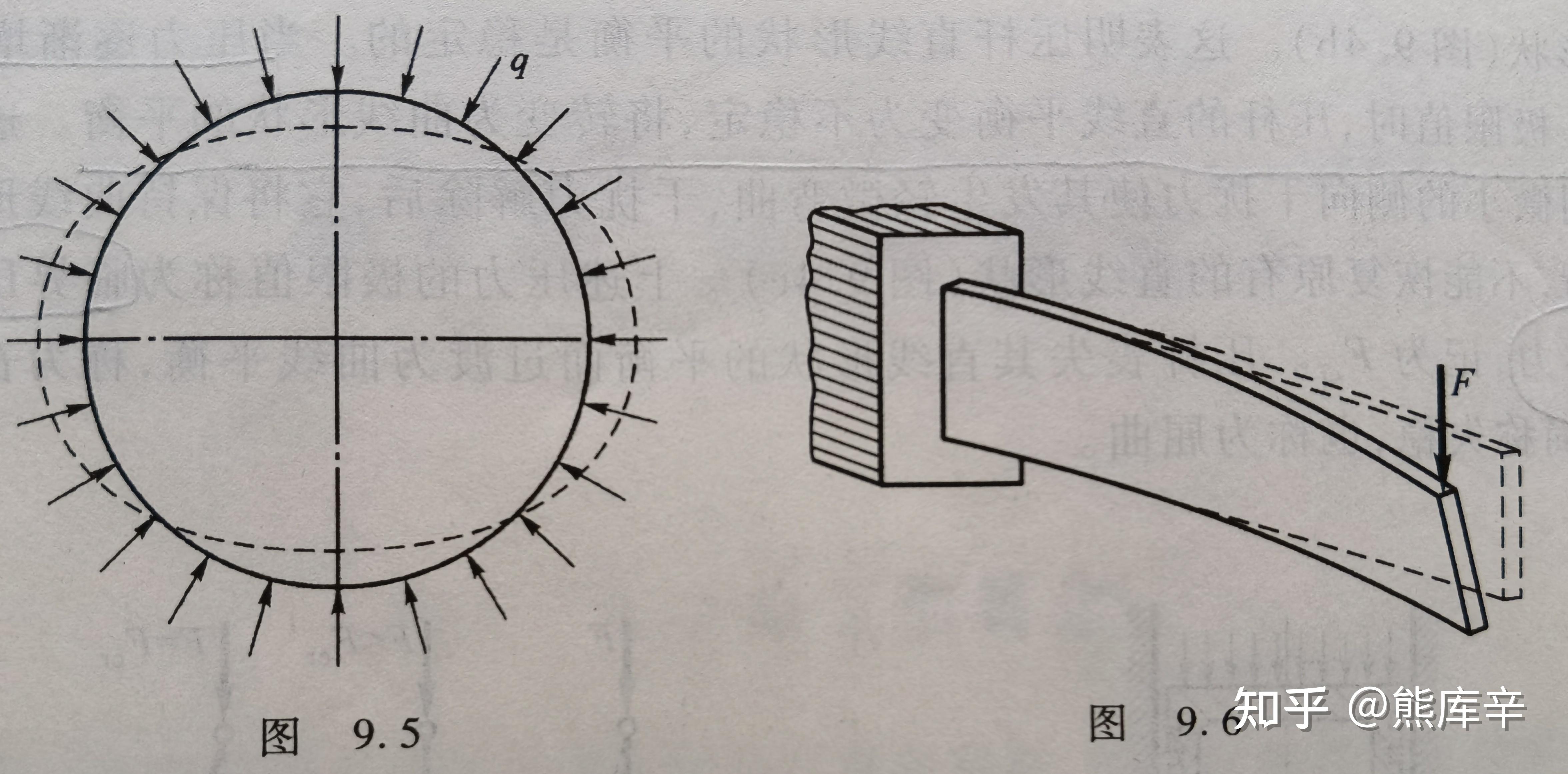
圆壳失稳+梁失稳
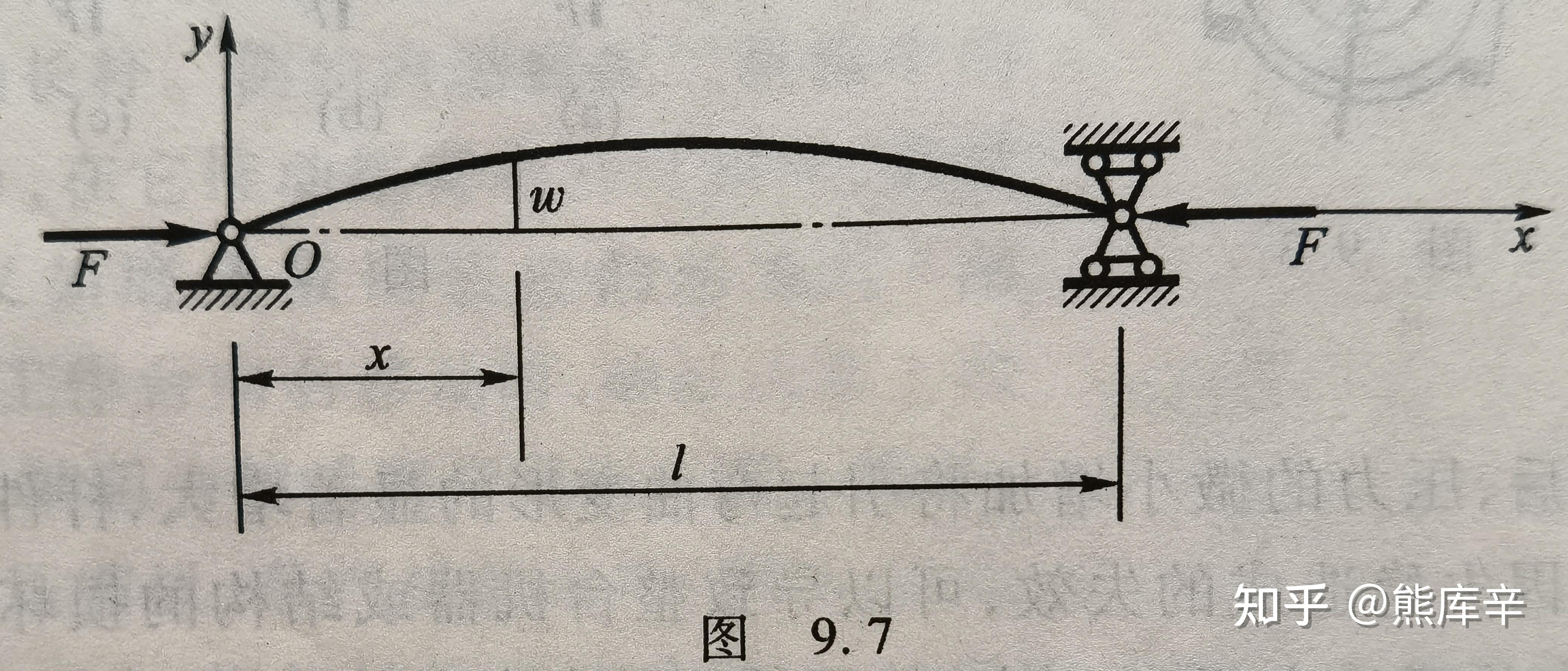
73、欧拉公式
细长杆两端球铰支座受压时,临界压力为 F_{cr}=\frac{\pi^2EI}{L^2} ,其中E为材料杨氏模量,I为惯性矩,L为杆的长度,此公式也称为两端铰支压杆的欧拉公式。
发动机进排气凸轮挺杆、活塞杆等压杆都可简化为两端铰支的受压杆。
临界压力计算
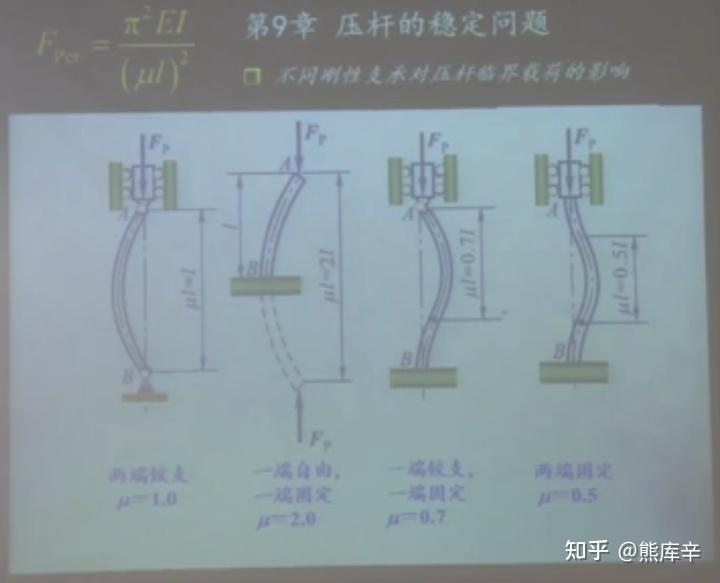
欧拉公式普遍形式: F_{cr}=\frac{\pi^2EI}{\mu l^2} ,其中\mu 为长度系数,各种约束条件下,长度系数取值如下,其他约束条件下的长度系数通常可由相关设计手册查询得到。

欧拉公式长度因数取值
一端固定一端自由,相当于两端铰支的一半形状,因此长度因数取2;
两端固定时,相当于中间的一半类似于两端铰支变形,因此长度因数取0.5;
一端固定,一端铰支,只有四分之三的长度相当于两端铰支变形,因此长度因数取0.7左右。
欧拉公式取值
74、欧拉公式适用范围
由于欧拉公式是由弯曲变形的近似微分方程\frac{d^2w}{dx^2}=\frac{M}{EI} 导出,材料服从胡克定律是上述微分方程的基础,因此只有临界应力小于比例极限时,屈服临界应力 \sigma_{cr}=\frac{F_{cr}}{A}=\frac{\pi^2EI}{(\mu l)^2A}=\frac{\pi^2E}{(\frac{\mu l}{i})^2}=\frac{\pi^2E}{\lambda^2}\leq\sigma_p 比例极限,欧拉公式才适用;其中 I=i^2A ,i为横截面的惯性半径, \lambda=\frac{\mu l}{i} 为长细比(柔度)。
\mu l 为等效长度, i 为截面等效半径(截面粗细),因此称 \lambda 为长细比。
适用范围判断准则:柔度λ大于极限值 \lambda_p ,即 \lambda \geq \lambda_p=\pi \sqrt{\frac{E}{\sigma_p}} , \sigma_p 为比例极限。
根据失效形式对杆进行分类:细长杆(大柔度杆),中长杆(中等柔度杆),短粗杆(小柔度杆),对应失效准则如下图所示。
细长杆: \lambda\geq\lambda_p=\pi \sqrt{\frac{E}{\sigma_p}} ,主要失效形式为屈曲失稳,根据欧拉公式计算屈曲失稳时的临界应力来判断是否失效;
中长杆: \lambda_0\leq\lambda\leq \lambda_p ,同时发生屈曲和塑性屈服,根据直线公式计算失效应力,根据 \sigma_s=\sigma_{cr}=a-b\lambda 计算 \lambda_0 ,用于判断是杆类型;
短粗杆: \lambda\leq\lambda_0=\frac{a-\sigma_s}{b} ,主要失效形式为塑性屈服,受压时先发生塑性屈服,然后产生裂纹,最后断裂。
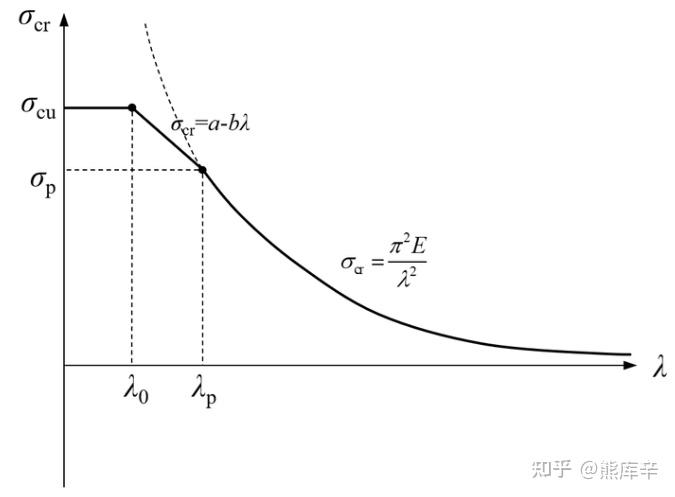
临界应力总图
杆件稳定性校核计算过程
- 根据\lambda = \frac{\mu l}{i} 计算杆件长细比
- 根据 \lambda_p=\pi \sqrt{\frac{E}{\sigma_p}} 计算临界应力总图中的 \lambda_p ,根据\lambda_0=\frac{a-\sigma_s}{b} 计算临界应力总图中的 \lambda_0 ,判断杆类型
- 根据杆类型,选择相应方法计算临界应力和临界载荷
- 将临界载荷与实际载荷对比,判断是否发生失稳
75、如何提升压杆稳定性?
- 选择合理的截面形状,从欧拉公式可以看出,惯性矩越大,临界压力也越大——较好方法
- 不增加截面面积时,尽可能将材料放在离截面形心较远处,从而得到更大的惯性矩和惯性半径,从而提高临界压力
- 截面面积相同的情况下,空心环形截面比实心圆截面合理
- 尽量选择中心对称的截面,使得截面对任意形心轴具有相近的惯性半径,从而保证截面在任一纵向平面内有相等或相近的稳定性;若截面在各平面内约束条件不同, \mu 取值不同,此时要求截面在不同平面内取不同的惯性半径,从而保证截面对各平面有相近的稳定性
- 发动机连杆在旋转平面可简化为铰支座\mu=1 ,在垂直于连杆的旋转平面内可简化为固定约束 \mu=0.5 ,此时要求垂直于旋转平面截面尺寸小于旋转平面,从而获得相近的稳定性
- 改变压杆约束条件,在杆中间位置增加支座,相当于减小杆长——操作简单也很实用, l^2 效果显著
- 选择杨氏模量较大的材料——通常价格昂贵
附录 截面几何性质
五种截面几何属性作用:
- 惯性矩:计算纯弯曲变形杆截面正应力,惯性矩越大,杆抵抗弯曲变形的能力越强;
- 极惯性矩:计算扭转变形杆截面切应力,极惯性矩越大,杆抵抗扭转变形的能力越强;
- 静矩:计算截面形心;
- 惯性积:惯性积等于零时对应的坐标系为主坐标系,此时惯性矩取最大和最小值;
- 惯性半径:计算压杆稳定性,惯性半径越大,受压杆件的失稳的临界应力越大,杆越不容易失稳。
关于截面几何性质的详细信息,可参考下面这篇文章。
<hr/>刘鸿文《材料力学》第五版上册笔记到此结束,我们下册再见。 |
|